Question

正四面体S—ABC中，E为SA的中点，F为的中心，则直线EF与平面ABC所成的角的正切值是                 。

Answer 1

 

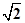
解析试题分析：连接SF，则SF⊥平面ABC．连接AF并延长交BC于H，取线段AF的中点G，连接EG，由E为SA的中点，则EG∥SF，∴EG⊥平面ABC，∴∠EFG即为EF与平面ABC所成的角． 
设正四面体的边长为a，则AH=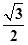a，且AF=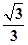a，
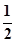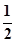在Rt△AGE中，AE=a，AG=AF=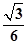a，∠EGA=90°，
∴EG=AE²-AG²=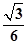a．在Rt△EGF中，FG=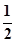AF=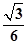a，EG=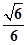a，∠EGF=90°，
∴tan∠EFG=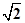
即EF与平面ABC所成的角的正切值是。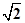
考点：本题主要考查立体几何中几何体的特征，角的计算。
点评：基础题，立体几何题，是高考必考内容，往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中，有“几何法”和“向量法”。利用几何法，要遵循“一作、二证、三计算”的步骤，本题中先做出线面角，再证出线面角，最后把角放到一个三角形中解出结果。