练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】红队队员甲、乙、丙与蓝队队员A、B、C进行围棋比赛，甲对A，乙对B，丙对C各一盘，已知甲胜A，乙胜B，丙胜C的概率分别为，，，假设各盘比赛结果相互独立．

    （I）求红队至少两名队员获胜的概率；

    （II）用表示红队队员获胜的总盘数，求的分布列和数学期望．

    【答案】（Ⅰ）；（Ⅱ）详见解析

    【解析】

    解：（I）设甲胜A的事件为D，乙胜B的事件为E，丙胜C的事件为F，

    则分别表示甲不胜A、乙不胜B，丙不胜C的事件．

    因为，．

    红队至少两人获胜的事件有：，

    由于以上四个事件两两互斥且各盘比赛的结果相互独立，因此红队至少两人获胜的概率

    （II）由题意知可能的取值为0，1，2，3．

    又由（I）知是两两互斥事件，且各盘比赛的结果相互独立，

    因此，

    ，

    由对立事件的概率公式得

    所以的分布列为：











    因此

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，、、、分别是、、、的中点.

    （1）求证：、、、四点共面；

    （2）求证：平面平面；

    （3）若、分别为、的中点，求证：平面平面.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数y＝f(x)(x∈R)满足f(1+x)＝f(1-x)且x∈[－1，1]时，f(x)＝1－x2，函数g(x)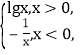＝则函数h(x)＝f(x)－g(x)在区间[－5，5]内的零点的个数为

    A. 7 B. 8 C. 9 D. 10

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某居民小区有两个相互独立的安全防范系统(简称系统)和，系统和在任意时刻发生故障的概率分别为和.

    （1）求在任意时刻至少有一个系统不发生故障的概率；

    （2）设系统在3次相互独立的检测中不发生故障的次数为随机变量，求的概率分布列及数学期望.(用数字作答)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，内角A，B，C的对边分别为a，b，c，已知.

    (1)求角C的值；

    (2)若c＝2，且△ABC的面积为，求a，b.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）是否存在实数、，使得函数的定义域和值域都是？若存在，请求出，的值；若不存在，请说明理由．

    （2）若存在实数，，使得函数的定义域是，值域是，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

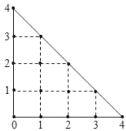
    【题目】某人在如图所示的直角边长为4米的三角形地块的每个格点（指纵、横直线的交叉点以及三角形的顶点）处都种了一株相同品种的作物．根据历年的种植经验，一株该种作物的年收货量(单位：kg)与它的“相近”作物株数之间的关系如下表所示：

    X

    1

    2

    3

    4

    Y

    51

    48

    45

    42

    这里，两株作物“相近”是指它们之间的直线距离不超过1米．

    （Ⅰ）完成下表,并求所种作物的平均年收获量;

    Y

    51

    48

    45

    42

    频数


    4



    (Ⅱ)在所种作物中随机选取一株,求它的年收获量至少为48kg的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）求曲线在点处的切线方程；

    （2）若关于的方程有三个不同的实根，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面是平行四边形， 平面，点， 分别为， 的中点，且， .

    （1）证明： 平面；

    （2）设直线与平面所成角为，当在内变化时，求二面角的取值范围.

    查看答案和解析>>

    同步练习册答案