练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知f(x)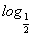＝(x2－ax＋3a)在区间[2，＋∞)上是减函数，则实数a的取值范围是(　　)

    A．(－4,4)                           B．[－4,4)

    C．(－4,4]                           D．[－4,4]


    C


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    y1＝40.9，y2＝log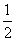4.3，y3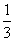＝()1.5，则(　　)

    A．y3＞y1＞y2                         B．y2＞y1＞y3

    C．y1＞y2＞y3                         D．y1＞y3＞y2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y＝1＋的零点是(　　)

    A．(－1,0)　　　　　　               B．x＝－1

    C．x＝1                              D．x＝0

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某公司今年1月份推出新产品A，其成本价为492元/件，经试销调查，销售量与销售价的关系如下表：

    销售价x(元/件)

    650

    662

    720

    800

    销售量y(件)

    350

    333

    281

    200

    由此可知，销售量y(件)与销售价x(元/件)可近似看作一次函数y＝kx＋b的关系(通常取表中相距较远的两组数据所得的一次函数较为精确)．

    试问：销售价定为多少时，1月份利润最大？并求最大利润和此时的销售量．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝的定义域为(　　)

    A．(－3,0]                           B．(－3,1]

    C．(－∞，－3)∪(－3,0]              D．(－∞，－3)∪(－3,1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    关于函数y＝2x2－2x－3有以下4个结论：

    ①定义域为(－∞，－1)∪(3，＋∞)；

    ②递增区间为[1，＋∞)；

    ③是非奇非偶函数；

    ④值域是(，＋∞)．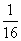

    则正确的结论是________．(填序号即可)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝

    (1)判断f(x)的奇偶性；

    (2)判断f(x)的单调性，并加以证明；

    (3)写出f(x)的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    判断下列函数是否存在零点，如果存在，请求出：

    (1)f(x)＝－8x2＋7x＋1；(2)f(x)＝x2＋x＋2；

    (3)f(x)＝x3＋1.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，如果sinA＝sinC，B＝30°，角B所对的边长b＝2，则△ABC的面积为(　　)

    A．4　　　　B．1　　　　C.　　　　D．2

    查看答案和解析>>

    同步练习册答案