
| A. | -ln 2 | B. | ln 2 | C. | 2$\sqrt{e}$-3 | D. | e2-3 |
分析 由g(m)=f (n),求出m的表达式,从而得出n-m的表达式,设h(x)=$\frac{{e}^{x-2}}{ln\frac{x\sqrt{e}}{2}}$,求得导数,求出单调区间和极小值,也为最小值,进而求出n-m的最小值.
解答 解:根据题意,g(m)=f (n)
即em-2=ln$\frac{n}{2}$+$\frac{1}{2}$,
∴m=2+ln(ln$\frac{n}{2}$+$\frac{1}{2}$),
∴n-m=n-2-ln(ln$\frac{n}{2}$+$\frac{1}{2}$),
=lnen-2-ln(ln$\frac{n}{2}$+$\frac{1}{2}$),
=ln$\frac{{e}^{n-2}}{ln\frac{n\sqrt{e}}{2}}$,
设h(x)=$\frac{{e}^{x-2}}{ln\frac{x\sqrt{e}}{2}}$,
则h′(x)=$\frac{{e}^{x-2}(ln\frac{x}{2}+\frac{1}{2}-\frac{1}{x})}{(ln\frac{x}{2}+\frac{1}{2})^{2}}$,
令h′(x)=0,得ln$\frac{x}{2}$+$\frac{1}{2}$-$\frac{1}{x}$=0,
由x>0,可得ln$\frac{x}{2}$+$\frac{1}{2}$-$\frac{1}{x}$递增,
当x=2时,h′(x)=0,
x>2时,h′(x)>0,h(x)递增;
0<x<2时,h′(x)<0,h(x)递减.
可得x=2处取得极小值且为最小值h(2)=2,
则n-m的最小值为ln2.
故选:B.
点评 本题考查了求函数最值的问题,解题的关键是建立目标函数,利用导数求目标函数的最值,是较难的题目.


科目:高中数学 来源: 题型:选择题
| A. | 60里 | B. | 48里 | C. | 36里 | D. | 24里 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 是否愿意提供志愿者服务 性别 | 愿意 | 不愿意 |
| 男生 | 30 | 10 |
| 女生 | 20 | 20 |
| P(K2≥k0) | 0.025 | 0.010 |
| k0 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{4}$个单位长度 | B. | 向右平移$\frac{π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{π}{4}$个单位长度 | D. | 向左平移$\frac{π}{12}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
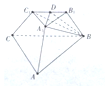 已知三棱台ABC-A1B1C1中,平面BB1C1C⊥平面ABC,∠ACB=90°,BB1=CC1=B1C1=2,BC=4,AC=6
已知三棱台ABC-A1B1C1中,平面BB1C1C⊥平面ABC,∠ACB=90°,BB1=CC1=B1C1=2,BC=4,AC=6查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | log2a>0 | B. | 2a-b<$\frac{1}{2}$ | C. | log2a+log2b<-2 | D. | 2($\frac{a}{b}$+$\frac{b}{a}$)<$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com