
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
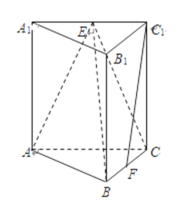
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)由直三棱柱侧棱与底面垂直可得![]() ,结合已知
,结合已知![]() ,得到
,得到![]() 平面
平面![]() ,从而得到平面
,从而得到平面![]() 平面
平面![]() ;
;
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() .由三角形中位线定理可得
.由三角形中位线定理可得![]() ,且
,且![]() ,得到四边形
,得到四边形![]() 为平行四边形,进一步得到
为平行四边形,进一步得到![]() .由线面平行的判定得到
.由线面平行的判定得到![]() 平面
平面![]() ;
;
(3)由已知求解直角三角形得到![]() ,求得底面积,代入三棱锥体积公式求得三棱锥
,求得底面积,代入三棱锥体积公式求得三棱锥![]() 的体积.
的体积.
解析:(1)证明:在三棱柱![]() 中,
中,
![]() 底面
底面![]() ,所以
,所以![]() .
.
又因为![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]()
(2)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() .
.
因为![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点,
的中点,
所以![]() ,且
,且![]() ,
,![]() .
.
因为![]() ,且
,且![]() ,所以
,所以![]() ,且
,且![]() ,
,
所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() .
.
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(3)因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() .
.
所以三棱锥![]() 的体积
的体积
![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
![]() 求椭圆的标准方程;
求椭圆的标准方程;
![]() 设直线l经过点
设直线l经过点![]() 且与椭圆C交于不同的两点M,N试问:在x轴上是否存在点Q,使得直线QM与直线QN的斜率的和为定值?若存在,求出点Q的坐标及定值,若不存在,请说明理由.
且与椭圆C交于不同的两点M,N试问:在x轴上是否存在点Q,使得直线QM与直线QN的斜率的和为定值?若存在,求出点Q的坐标及定值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右顶点分别为A,B,点P在椭圆O上运动,若△PAB面积的最大值为
的左、右顶点分别为A,B,点P在椭圆O上运动,若△PAB面积的最大值为![]() ,椭圆O的离心率为
,椭圆O的离心率为![]() .
.
(1)求椭圆O的标准方程;
(2)过B点作圆E:![]() 的两条切线,分别与椭圆O交于两点C,D(异于点B),当r变化时,直线CD是否恒过某定点?若是,求出该定点坐标,若不是,请说明理由.
的两条切线,分别与椭圆O交于两点C,D(异于点B),当r变化时,直线CD是否恒过某定点?若是,求出该定点坐标,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某品种一批树苗生长情况,在该批树苗中随机抽取了容量为120的样本,测量树苗高度(单位:![]() ,经统计,其高度均在区间
,经统计,其高度均在区间![]() ,
,![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,制成如图所示的频率分布直方图.其中高度为
分成6组,制成如图所示的频率分布直方图.其中高度为![]() 及以上的树苗为优质树苗.
及以上的树苗为优质树苗.

(1)求图中![]() 的值,并估计这批树苗的平均高度(同一组中的数据用该组区间的中点值作代表);
的值,并估计这批树苗的平均高度(同一组中的数据用该组区间的中点值作代表);
(2)已知所抽取的这120棵树苗来自于![]() ,
,![]() 两个试验区,部分数据如下列联表:
两个试验区,部分数据如下列联表:
|
| 合计 | |
优质树苗 | 20 | ||
非优质树苗 | 60 | ||
合计 |
将列联表补充完整,并判断是否有![]() 的把握认为优质树苗与
的把握认为优质树苗与![]() ,
,![]() 两个试验区有关系,并说明理由.
两个试验区有关系,并说明理由.
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() .
.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有5名男生和3名女生站成一排照相,
(1)3名女生站在一起,有多少种不同的站法?
(2)3名女生次序一定,但不一定相邻,有多少种不同的站法?
(3)3名女生不站在排头和排尾,也互不相邻,有多少种不同的站法?
(4)3名女生中,A,B要相邻,A,C不相邻,有多少种不同的站法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与x轴负半轴交于
与x轴负半轴交于![]() ,离心率
,离心率![]() .
.
(1)求椭圆C的方程;
(2)设直线![]() 与椭圆C交于
与椭圆C交于![]() 两点,连接AM,AN并延长交直线x=4于
两点,连接AM,AN并延长交直线x=4于![]() 两点,若
两点,若![]() ,直线MN是否恒过定点,如果是,请求出定点坐标,如果不是,请说明理由.
,直线MN是否恒过定点,如果是,请求出定点坐标,如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年全国“两会”,即中华人民共和国第十三届全国人大二次会议和中国人民政治协商会议第十三届全国委员会第二次会议,分别于2019年3月5日和3月3日在北京召开.为了了解哪些人更关注“两会”,某机构随机抽取了年龄在15~75岁之间的200人进行调查,并按年龄绘制的频率分布直方图如下图所示,把年龄落在区间[15,35)和[35,75]内的人分别称为“青少年人”和“中老年人”.经统计“青少年人”和“中老年人”的人数之比为19:21.其中“青少年人”中有40人关注“两会”,“中老年人”中关注“两会”和不关注“两会”的人数之比是2:1.
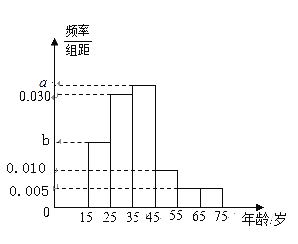
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)现采用分层抽样在[25,35)和[45,55)中随机抽取8名代表,从8人中任选2人,求2人中至少有1个是“中老年人”的概率是多少?
(Ⅲ)根据已知条件,完成下面的2×2列联表,并根据此统计结果判断:能否有99.9%的把握认为“中老年人”比“青少年人”更加关注“两会”?
关注 | 不关注 | 合计 | |
青少年人 | |||
中老年人 | |||
合计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com