
分析 根据条件求出与an的有关的关系式,利用条件,{an}单调递增,建立条件,即可得到结论.
解答 解:由条件Sn-1+Sn=2n2+1(n≥2)得Sn+Sn+1=2(n+1)2+1,
两式相减得an+1+an=4n+2,
故an+2+an+1=4n+6,两式再相减得an+2-an=4,得{an+2}是公差d=4的等差数列,
由n=2得a1+a2+a1=9,a2=9-2x,
从而a2n=4n+5-2x;
n=3得a1+a2+a3+a1+a2=19,a3=1+2x,从而a2n+1=4n-3+2x,
由条件得$\left\{\begin{array}{l}{x<9-2x}\\{4n+5-2x<4n-3+2x}\\{4n-3+2x<4(n+1)+5-2x}\end{array}\right.$,
解得2<x<3,
故x的取值范围为(2,3),
故答案为:(2,3).
点评 本题主要考查参数的取值范围的求解,根据条件求出与an的有关的关系式是解决本题的关键,有一定的难度.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>b>a | C. | b>c>a | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
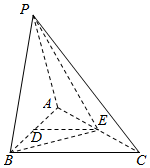 如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四面体ABCD中,CD=CB,AD⊥BD,点E,F分别是AB,BD的中点.
如图,在四面体ABCD中,CD=CB,AD⊥BD,点E,F分别是AB,BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
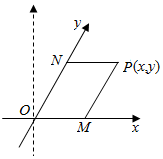 如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M,N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为x2+y2+xy-1=0.
如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M,N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为x2+y2+xy-1=0.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
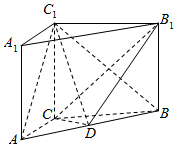 如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A∩B=B | B. | A∪B=A | C. | A?B | D. | ∁RA=B |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 196 | 197 | 200 | 203 | 204 |
| y | 1 | 3 | 6 | 7 | m |
| A. | 8.3 | B. | 8.2 | C. | 8.1 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com