
(本题满分12分)已知p: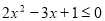 ,q:
,q: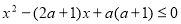
(1)若a=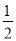 ,且
,且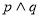 为真,求实数x的取值范围.
为真,求实数x的取值范围.
(2)若p是q的充分不必要条件,求实数a的取值范围.
(1)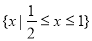 ;(2)
;(2)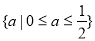 .
.
【解析】
试题分析:(1)先化简命题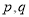 对应的集合,再利用真值表判定
对应的集合,再利用真值表判定 各自的真假,利用相应数集进行求解;(2)利用小范围是大范围的充分不必要条件转化为集合间的包含关系进行求解.
各自的真假,利用相应数集进行求解;(2)利用小范围是大范围的充分不必要条件转化为集合间的包含关系进行求解.
解题思路:1.符合命题的真值表:当且仅当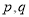 都为真命题时,
都为真命题时,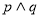 为真命题;当且仅当
为真命题;当且仅当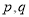 都为假命题时,
都为假命题时,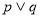 为假命题;命题
为假命题;命题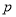 与命题
与命题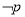 真假性相反;
真假性相反;
2.小范围是大范围的充分不必要条件.
试题解析:(1)∵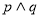 为真
为真
∴p真q真 1分
P真:则设A={x|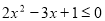 }=
}=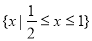 , 2分
, 2分
q真:B={x|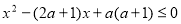 }=
}=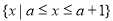 3分
3分
∵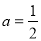 ∴B=
∴B=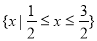 4分
4分
∴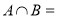
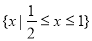
∴实数x的取值范围为: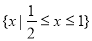 6分
6分
(2)由(1)知设A={x|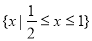 ,B=
,B=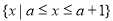
∵p是q的充分不必要条件,
∴A是B的真子集 8分
∴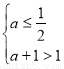 或
或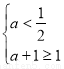 解得
解得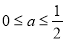 , 11分
, 11分
∴实数a的取值范围为: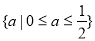 . 12分.
. 12分.
考点:1.复合命题的真值表;2.充分条件与必要条件.


科目:高中数学 来源:2014-2015学年海市松江区高三上学期期末考试文科数学试卷(解析版) 题型:解答题
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分
(文)对于曲线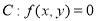 ,若存在非负实数
,若存在非负实数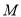 和
和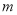 ,使得曲线
,使得曲线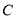 上任意一点
上任意一点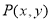 ,
,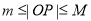 恒成立(其中
恒成立(其中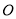 为坐标原点),则称曲线
为坐标原点),则称曲线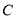 为有界曲线,且称
为有界曲线,且称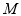 的最小值
的最小值 为曲线
为曲线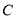 的外确界,
的外确界,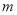 的最大值
的最大值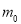 为曲线
为曲线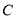 的内确界.
的内确界.
(1)写出曲线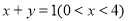 的外确界
的外确界 与内确界
与内确界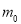 ;
;
(2)曲线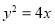 与曲线
与曲线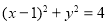 是否为有界曲线?若是,求出其外确界与内确界;若不是,请说明理由;
是否为有界曲线?若是,求出其外确界与内确界;若不是,请说明理由;
(3)已知曲线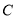 上任意一点
上任意一点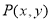 到定点
到定点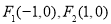 的距离之积为常数
的距离之积为常数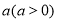 ,求曲线
,求曲线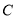 的外确界与内确界.
的外确界与内确界.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省高一上学期期中考试数学试卷(解析版) 题型:选择题
定义在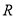 上的增函数
上的增函数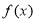 满足
满足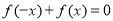 ,
,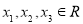 ,且
,且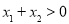 ,
,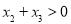 ,
,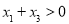 ,则
,则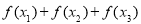 的值( )
的值( )
A.一定大于0 B.一定小于0 C.等于0 D.正负都有可能
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省乐陵市高二上学期期中考试文科数学试卷(解析版) 题型:选择题
在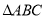 中,已知
中,已知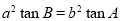 ,则该
,则该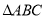 的形状为( )
的形状为( )
A、等腰三角形 B、直角三角形
C、正三角形 D、等腰或直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com