
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分
(文)对于曲线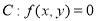 ,若存在非负实数
,若存在非负实数 和
和 ,使得曲线
,使得曲线 上任意一点
上任意一点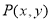 ,
,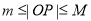 恒成立(其中
恒成立(其中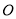 为坐标原点),则称曲线
为坐标原点),则称曲线 为有界曲线,且称
为有界曲线,且称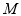 的最小值
的最小值 为曲线
为曲线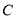 的外确界,
的外确界,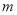 的最大值
的最大值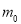 为曲线
为曲线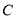 的内确界.
的内确界.
(1)写出曲线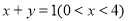 的外确界
的外确界 与内确界
与内确界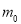 ;
;
(2)曲线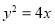 与曲线
与曲线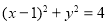 是否为有界曲线?若是,求出其外确界与内确界;若不是,请说明理由;
是否为有界曲线?若是,求出其外确界与内确界;若不是,请说明理由;
(3)已知曲线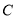 上任意一点
上任意一点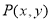 到定点
到定点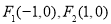 的距离之积为常数
的距离之积为常数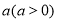 ,求曲线
,求曲线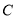 的外确界与内确界.
的外确界与内确界.
(1) 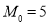
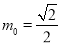 (2)
(2) 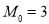 ,
,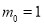 (3) 外确界
(3) 外确界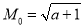 ,内确界
,内确界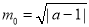 .
.
【解析】
试题分析:(1)根据信息外确界与内确界,即原点到曲线的最大值与最小值,曲线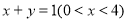 的外确界
的外确界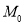 与内确界
与内确界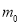 ,即原点到直线
,即原点到直线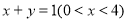 的最大值与最小值,易得答案;(2)看曲线
的最大值与最小值,易得答案;(2)看曲线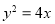 与曲线
与曲线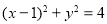 是否为有界曲线,即看此曲线上的点与原点的距离是否即有最大值又有最小值;(3)根据曲线
是否为有界曲线,即看此曲线上的点与原点的距离是否即有最大值又有最小值;(3)根据曲线 上任意一点
上任意一点 到定点
到定点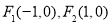 的距离之积为常数
的距离之积为常数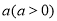 ,求出曲线
,求出曲线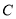 的方程,求外确界与内确界时,注意分类讨论的思想.
的方程,求外确界与内确界时,注意分类讨论的思想.
试题解析:(1)曲线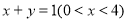 的外确界
的外确界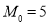 与内确界
与内确界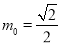 . 4分
. 4分
(2)对于曲线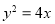 ,设
,设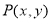 为曲线上任意一点
为曲线上任意一点
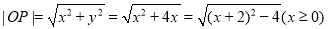
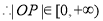
 曲线
曲线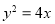 不是有界曲线. 7分
不是有界曲线. 7分
对于曲线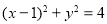
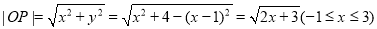
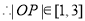
 曲线
曲线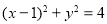 是有界曲线.外确界
是有界曲线.外确界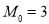 与内确界
与内确界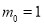 10分
10分
(3)由已知得: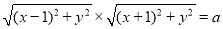 12分
12分
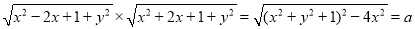
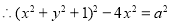
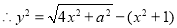
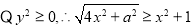
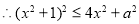
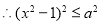
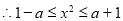
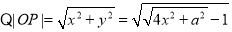 14分
14分
若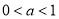 ,则
,则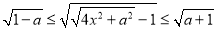 ,外确界
,外确界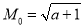 ,内确界
,内确界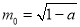 16分
16分
若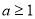 ,
,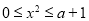 ,则
,则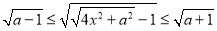 ,外确界
,外确界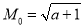 ,内确界
,内确界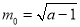
综合得:外确界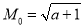 ,内确界
,内确界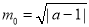 . 18分.
. 18分.
考点:曲线外确界与内确界的求法.


科目:高中数学 来源:2014-2015学年广东省潮州市高三上学期期末教学质量检测理科数学试卷(解析版) 题型:选择题
已知数列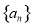 为等比数列,且
为等比数列,且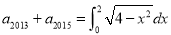 ,则
,则 的值为( )
的值为( )
A.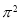 B.
B.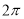 C.
C.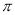 D.
D.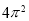
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省高密市高三12月检测理科数学试卷(解析版) 题型:选择题
将函数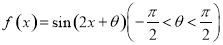 的图象向右平移
的图象向右平移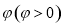 个单位长度后得到函数
个单位长度后得到函数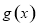 的图象,若
的图象,若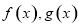 的图象都经过点
的图象都经过点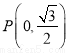 ,则
,则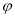 的值可以是
的值可以是
A.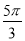 B.
B.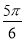 C.
C.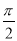 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省、湘阴县一中高三12月联考理科数学试卷(解析版) 题型:选择题
若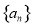 是等差数列,则下列数列中仍为等差数列的个数有 ( )
是等差数列,则下列数列中仍为等差数列的个数有 ( )
①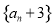 , ②
, ②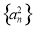 , ③
, ③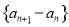 , ④
, ④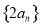 , ⑤
, ⑤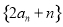 .
.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源:2014-2015学年海市松江区高三上学期期末考试文科数学试卷(解析版) 题型:选择题
已知满足条件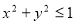 的点
的点 构成的平面区域面积为
构成的平面区域面积为 ,满足条件
,满足条件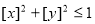 的点
的点 构成的平面区域的面积为
构成的平面区域的面积为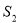 ,其中
,其中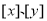 分别表示不大于
分别表示不大于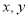 的最大整数,例如:
的最大整数,例如: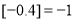 ,
,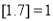 ,则
,则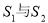 的关系是
的关系是
A.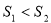 B.
B.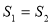
C.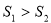 D.
D.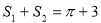
查看答案和解析>>
科目:高中数学 来源:2014-2015学年海市松江区高三上学期期末考试文科数学试卷(解析版) 题型:填空题
从0,1,2,3,4,5,6,7,8,9中任取七个不同的数,则这七个数的中位数是5的概率为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年海市松江区高三上学期期末考试理科数学试卷(解析版) 题型:选择题
若二项式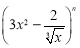
 展开式中含有常数项,则
展开式中含有常数项,则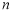 的最小取值是
的最小取值是
A.4 B.5
C.6 D.7
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省乐陵市高二上学期期中考试理科数学试卷(解析版) 题型:解答题
(本题满分12分)已知p: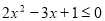 ,q:
,q: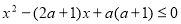
(1)若a=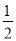 ,且
,且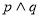 为真,求实数x的取值范围.
为真,求实数x的取值范围.
(2)若p是q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com