
科目:高中数学 来源:2014-2015学年湖北省毕业生二月调研考试理科数学试卷(解析版) 题型:填空题
(选修4-1:几何证明选讲)如图,已知直线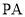 切圆
切圆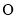 于点
于点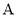 ,直线
,直线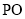 交圆
交圆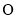 于点
于点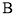 、
、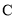 ,若
,若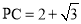 ,
,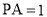 ,则圆
,则圆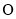 的半径长为 .
的半径长为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省潮州市高三上学期期末教学质量检测文科数学试卷(解析版) 题型:解答题
(本小题满分13分)从一批草莓中,随机抽取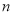 个,其重量(单位:克)的频率分布表如下:
个,其重量(单位:克)的频率分布表如下:
分组(重量) |
|
|
|
|
频数(个) |
|
|
|
|
已知从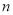 个草莓中随机抽取一个,抽到重量在
个草莓中随机抽取一个,抽到重量在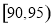 的草莓的概率为
的草莓的概率为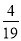 .
.
(1)求出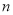 ,
,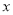 的值;
的值;
(2)用分层抽样的方法从重量在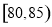 和
和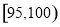 的草莓中共抽取
的草莓中共抽取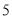 个,再从这
个,再从这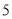 个草莓中任取
个草莓中任取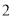 个,求重量在
个,求重量在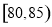 和
和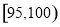 中各有
中各有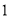 个的概率.
个的概率.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省潮州市高三上学期期末教学质量检测理科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知椭圆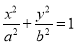 (
(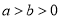 )经过点
)经过点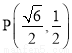 ,离心率为
,离心率为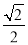 ,动点
,动点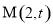 (
(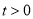 ).
).
(1)求椭圆的标准方程;
(2)求以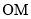 (
(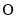 为坐标原点)为直径且被直线
为坐标原点)为直径且被直线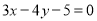 截得的弦长为
截得的弦长为 的圆的方程;
的圆的方程;
(3)设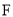 是椭圆的右焦点,过点
是椭圆的右焦点,过点 作
作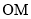 的垂线与以
的垂线与以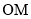 为直径的圆交于点
为直径的圆交于点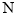 ,证明线段
,证明线段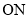 的长为定值,并求出这个定值.
的长为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省高密市高三12月检测文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知函数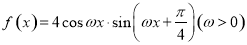 的最小正周期为
的最小正周期为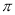 .
.
(Ⅰ)求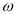 的值;
的值;
(Ⅱ)讨论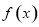 在区间
在区间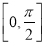 上的单调性.
上的单调性.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省高密市高三12月检测理科数学试卷(解析版) 题型:解答题
(本小题满分13分)已知椭圆 的离心率为
的离心率为 ,右焦点
,右焦点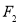 到直线
到直线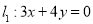 的距离为
的距离为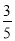 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过椭圆右焦点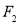 斜率为
斜率为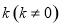 的直线
的直线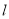 与椭圆C相交于E、F两点,A为椭圆的右顶点,直线AE,AF分别交直线
与椭圆C相交于E、F两点,A为椭圆的右顶点,直线AE,AF分别交直线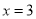 于点M,N,线段MN的中点为P,记直线
于点M,N,线段MN的中点为P,记直线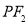 的斜率为
的斜率为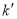 ,求证:
,求证: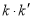 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年海市松江区高三上学期期末考试文科数学试卷(解析版) 题型:解答题
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分
(文)对于曲线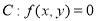 ,若存在非负实数
,若存在非负实数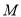 和
和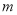 ,使得曲线
,使得曲线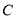 上任意一点
上任意一点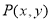 ,
,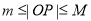 恒成立(其中
恒成立(其中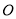 为坐标原点),则称曲线
为坐标原点),则称曲线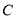 为有界曲线,且称
为有界曲线,且称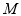 的最小值
的最小值 为曲线
为曲线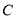 的外确界,
的外确界,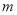 的最大值
的最大值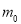 为曲线
为曲线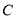 的内确界.
的内确界.
(1)写出曲线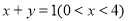 的外确界
的外确界 与内确界
与内确界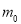 ;
;
(2)曲线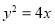 与曲线
与曲线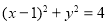 是否为有界曲线?若是,求出其外确界与内确界;若不是,请说明理由;
是否为有界曲线?若是,求出其外确界与内确界;若不是,请说明理由;
(3)已知曲线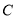 上任意一点
上任意一点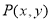 到定点
到定点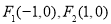 的距离之积为常数
的距离之积为常数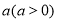 ,求曲线
,求曲线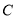 的外确界与内确界.
的外确界与内确界.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com