
分析 ①利用和角的正切公式,即可得出结论;②当λ=-4时,$\overrightarrow{a}$与$\overrightarrow{b}$同向,不符合;
③设BC的中点为D,动点P满足$\overrightarrow{OP}$=$\overrightarrow{OA}$+$λ(\overrightarrow{AB}+\overrightarrow{AC})$=$\overrightarrow{OA}$+2λ$\overrightarrow{OD}$,即可得出结论;
④解题突破口是从已知条件所给的关系式化简,确定出2$\overrightarrow{PA}$=$\overrightarrow{CP}$,即点P是CA边上的第二个三等分点,由此问题可解.
解答 解:①因为α+β=$\frac{7π}{4}$,所以tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=-1,所以,tanα+tanβ=-1+tanαtanβ
即:2=1-tanα-tanβ+tanαtanβ=(1-tanα)(1-tanβ),故正确;
②∵$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为锐角,∴$\overrightarrow{a}$•$\overrightarrow{b}$>0,即2-2λ>0,解得λ<1;当λ=-4时,$\overrightarrow{a}$与$\overrightarrow{b}$同向,∴实数λ的取值范围是(-∞,-4)∪(-4,1),故不正确;
③设BC的中点为D,动点P满足$\overrightarrow{OP}$=$\overrightarrow{OA}$+$λ(\overrightarrow{AB}+\overrightarrow{AC})$=$\overrightarrow{OA}$+2λ$\overrightarrow{OD}$,则P的轨迹一定通过△ABC的重心,故正确;
④在△ABC所在的平面上有一点P,满足$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{AB}$,即$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{BA}$+$\overrightarrow{PC}$=$\overrightarrow{0}$,得$\overrightarrow{PA}$+$\overrightarrow{PA}$+$\overrightarrow{PC}$=$\overrightarrow{0}$,即2$\overrightarrow{PA}$=$\overrightarrow{CP}$,所以点P是CA边上的第二个三等分点,故△PBC与△ABC的面积之比是2:3,故不正确.
故答案为:①③.
点评 本题考查命题的真假判断,涉及和角的正切公式,向量知识的运用,考查学生分析解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
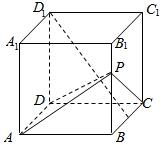 在边长为a的正方体ABCD-A1B1C1D1中,点P从B点开始按路径B→B1→C1→C运动,设从B点列P点的路程为x,V(x)表示空间几何体的体积,其中四校锥P-ABCD的体积为V1(x),剩余空间几何体的体积为V2(x).则f(x)=$\frac{{V}_{1}(x)}{{V}_{2}(x)}$的图象为( )
在边长为a的正方体ABCD-A1B1C1D1中,点P从B点开始按路径B→B1→C1→C运动,设从B点列P点的路程为x,V(x)表示空间几何体的体积,其中四校锥P-ABCD的体积为V1(x),剩余空间几何体的体积为V2(x).则f(x)=$\frac{{V}_{1}(x)}{{V}_{2}(x)}$的图象为( )| A. | 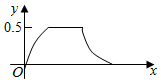 | B. | 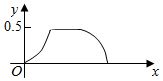 | ||
| C. | 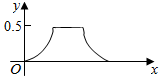 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com