
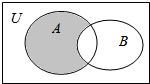
分析 (1)根据图形便可看出,阴影部分表示A∩B在A中的补集,用符号表示出来即可;
(2)C⊆B,从而C=∅时可以,并可求出对应的a的范围而C≠∅时;则a应满足$\left\{\begin{array}{l}{2a<a+1}\\{2a≥-2}\\{a+1≤14}\end{array}\right.$,解出a的范围,再并上前面a的范围即可得到实数a的取值范围.
解答 解:(1)可以看出,阴影部分表示A,B交集在A中的补集,表示为:∁A(A∩B);
(2)①若C=∅,满足C⊆B,则:2a≥a+1;
∴a≥1;
②若C≠∅,则a满足:
$\left\{\begin{array}{l}{2a<a+1}\\{2a≥-2}\\{a+1≤14}\end{array}\right.$;
解得-1≤a<1;
∴a≥-1;
∴实数a的取值范围为[-1,+∞).
点评 考查交集、补集的概念及其运算,空集的概念,以及子集的概念,不要漏了C=∅的情况.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3.4,0) | B. | (13,0) | C. | (5,0) | D. | (1,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com