
ЁОЬтФПЁПФГГЇЩњВњВЛЭЌЙцИёЕФвЛжжВњЦЗЃЌИљОнМьВтБъзМЃЌЦфКЯИёВњЦЗЕФжЪСП![]() гыГпДч
гыГпДч![]() жЎМфНќЫЦТњзуЙиЯЕЪН
жЎМфНќЫЦТњзуЙиЯЕЪН![]() ЮЊДѓгк0ЕФГЃЪ§).АДееФГЯюжИБъВтЖЈЃЌЕБВњЦЗжЪСПгыГпДчЕФБШдкЧјМф
ЮЊДѓгк0ЕФГЃЪ§).АДееФГЯюжИБъВтЖЈЃЌЕБВњЦЗжЪСПгыГпДчЕФБШдкЧјМф![]() ФкЪБЮЊгХЕШЦЗ.ЯжЫцЛњГщШЁ6МўКЯИёВњЦЗЃЌВтЕУЪ§ОнШчЯТ:
ФкЪБЮЊгХЕШЦЗ.ЯжЫцЛњГщШЁ6МўКЯИёВњЦЗЃЌВтЕУЪ§ОнШчЯТ:
ГпДч | 38 | 48 | 58 | 68 | 78 | 88 |
жЪСП | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
жЪСПгыГпДчЕФБШ | 0.442 | 0.392 | 0.367 | 0.329 | 0.308 | 0.290 |
(I)ЯжДгГщШЁЕФ6МўКЯИёВњЦЗжадйШЮбЁ3МўЃЌМЧ![]() ЮЊШЁЕНгХЕШЦЗЕФМўЪ§ЃЌЪдЧѓЫцЛњБфСП
ЮЊШЁЕНгХЕШЦЗЕФМўЪ§ЃЌЪдЧѓЫцЛњБфСП![]() ЕФЗжВМСаКЭЦкЭћ;
ЕФЗжВМСаКЭЦкЭћ;
(II)ИљОнВтЕУЪ§ОнзїСЫГѕВНДІРэЃЌЕУЯрЙиЭГМЦСПЕФжЕШчЯТБэ:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(i)ИљОнЫљИјЭГМЦСПЃЌЧѓ![]() Йигк
Йигк![]() ЕФЛиЙщЗНГЬ;
ЕФЛиЙщЗНГЬ;
(ii)вбжЊгХЕШЦЗЕФЪевц![]() (ЕЅЮЛ:ЧЇдЊ)гы
(ЕЅЮЛ:ЧЇдЊ)гы![]() ЕФЙиЯЕЮЊ
ЕФЙиЯЕЮЊ![]() ЃЌдђЕБгХЕШЦЗЕФГпДч
ЃЌдђЕБгХЕШЦЗЕФГпДч![]() ЮЊКЮжЕЪБЃЌЪевц
ЮЊКЮжЕЪБЃЌЪевц![]() ЕФдЄБЈжЕзюДѓ? (ОЋШЗЕН0.1)
ЕФдЄБЈжЕзюДѓ? (ОЋШЗЕН0.1)
ИН:ЖдгкбљБО![]() ЃЌ ЦфЛиЙщжБЯп
ЃЌ ЦфЛиЙщжБЯп![]() ЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЙЋЪНЗжБ№ЮЊЃК
ЕФаБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЙЋЪНЗжБ№ЮЊЃК
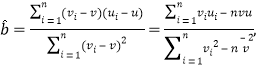
![]()
![]()
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЈ2ЃЉ(i)![]() ЃЌ(ii)
ЃЌ(ii)![]()
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉвЊЧѓЫцЛњБфСП![]() ЕФЗжВМСаЃЌгІЯШШЗЖЈГщШЁЕФ6МўКЯИёВњЦЗжаЃЌгХЕШЦЗЕФМўЪ§ЃЌгІШЗЖЈЧјМф
ЕФЗжВМСаЃЌгІЯШШЗЖЈГщШЁЕФ6МўКЯИёВњЦЗжаЃЌгХЕШЦЗЕФМўЪ§ЃЌгІШЗЖЈЧјМф![]() ЕФДѓжТЗЖЮЇЃЌМД
ЕФДѓжТЗЖЮЇЃЌМД![]() ЁЃНјЖјгЩГщШЁ6МўКЯИёВњЦЗЕФВтЕУЪ§ОнПЩЕУга3МўЮЊгХЕШЦЗЃЌ3МўЮЊЗЧгХЕШЦЗЁЃЫљвдШЁЕНгХЕШЦЗЕФМўЪ§
ЁЃНјЖјгЩГщШЁ6МўКЯИёВњЦЗЕФВтЕУЪ§ОнПЩЕУга3МўЮЊгХЕШЦЗЃЌ3МўЮЊЗЧгХЕШЦЗЁЃЫљвдШЁЕНгХЕШЦЗЕФМўЪ§![]() ЃЌНјЖјЧѓетЫФжжШЁжЕЪБЕФИХТЪЃЌНјЖјПЩЕУЗжВМСаЁЃгУЦкЭћЙЋЪНМДПЩЧѓЕУЦкЭћЁЃЃЈ2ЃЉ(i)вђЮЊ
ЃЌНјЖјЧѓетЫФжжШЁжЕЪБЕФИХТЪЃЌНјЖјПЩЕУЗжВМСаЁЃгУЦкЭћЙЋЪНМДПЩЧѓЕУЦкЭћЁЃЃЈ2ЃЉ(i)вђЮЊ![]() жаЕФ
жаЕФ![]() гы
гы![]() жЎМфВЛЪЧжБЯпадЛиЙщЙиЯЕЃЌЙЪСНБпШЁЖдЪ§ПЩЕУ
жЎМфВЛЪЧжБЯпадЛиЙщЙиЯЕЃЌЙЪСНБпШЁЖдЪ§ПЩЕУ![]() ЃЌЛЛдЊСю
ЃЌЛЛдЊСю![]() ЃЌЕУ
ЃЌЕУ![]() Чв
Чв![]() ЃЌИљОнЬтжаЫљИјЕФБэжаЪ§ОнПЩЧѓГі
ЃЌИљОнЬтжаЫљИјЕФБэжаЪ§ОнПЩЧѓГі
![]() НјЖјПЩЧѓЕУ
НјЖјПЩЧѓЕУ![]() ЧѓЕУ
ЧѓЕУ![]()
ЫљЧѓ![]() Йигк
Йигк![]() ЕФЛиЙщЗНГЬЮЊ
ЕФЛиЙщЗНГЬЮЊ![]() ЁЃ(ii)вЊЧѓЕБгХЕШЦЗЕФГпДч
ЁЃ(ii)вЊЧѓЕБгХЕШЦЗЕФГпДч![]() ЮЊКЮжЕЪБЃЌЪевц
ЮЊКЮжЕЪБЃЌЪевц![]() ЕФдЄБЈжЕзюДѓЁЃгІгУ
ЕФдЄБЈжЕзюДѓЁЃгІгУ![]() РДБэЪОЪевц
РДБэЪОЪевц![]() ЁЃЙЪНЋ
ЁЃЙЪНЋ![]() ДњШы
ДњШы![]() ПЩЕУ
ПЩЕУ![]() ЁЃ
ЁЃ
ПЩСю![]() ЃЌдђ
ЃЌдђ![]() ПЩБфЮЊ
ПЩБфЮЊ![]() ЃЌетИіЪЧЙигк
ЃЌетИіЪЧЙигк![]() ЕФЖўДЮКЏЪ§ЃЌвЊЧѓЦфзюДѓжЕЃЌгІЯШЧѓздБфСП
ЕФЖўДЮКЏЪ§ЃЌвЊЧѓЦфзюДѓжЕЃЌгІЯШЧѓздБфСП![]() ЕФШЁжЕЗЖЮЇЁЃгЩгХЕШЦЗжЪСПгыГпДчЕФБШПЩЧѓЕУ
ЕФШЁжЕЗЖЮЇЁЃгЩгХЕШЦЗжЪСПгыГпДчЕФБШПЩЧѓЕУ ЃЌНјЖјПЩЕУ
ЃЌНјЖјПЩЕУ![]() ЃЌМД
ЃЌМД![]() ЁЃНЋ
ЁЃНЋ![]() ХфЗНПЩЕУ
ХфЗНПЩЕУ![]() ЁЃгЩЖўДЮКЏЪ§ЕФаджЪПЩжЊЕБ
ЁЃгЩЖўДЮКЏЪ§ЕФаджЪПЩжЊЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ШЁзюДѓжЕЁЃНјЖјПЩЧѓЕБгХЕШЦЗЕФГпДч
ШЁзюДѓжЕЁЃНјЖјПЩЧѓЕБгХЕШЦЗЕФГпДч![]() ЃЌЪевц
ЃЌЪевц![]() ЕФдЄБЈжЕзюДѓЁЃ
ЕФдЄБЈжЕзюДѓЁЃ
ЯъНтЃКЃЈ1ЃЉНтЃКгЩвбжЊЃЌгХЕШЦЗЕФжЪСПгыГпДчЕФБШдкЧјМф![]() ФкЃЌМД
ФкЃЌМД![]()
дђЫцЛњГщШЁЕФ6МўКЯИёВњЦЗжаЃЌга3МўЮЊгХЕШЦЗЃЌ3МўЮЊЗЧгХЕШЦЗ
ЯжДгГщШЁЕФ6МўКЯИёВњЦЗжадйШЮбЁ3МўЃЌдђШЁЕНгХЕШЦЗЕФМўЪ§![]()
![]()
![]()
![]()
![]()
![]() ЕФЗжВМСаЮЊ
ЕФЗжВМСаЮЊ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]()
ЃЈ2ЃЉНтЃК(i)Жд![]() СНБпШЁздШЛЖдЪ§ЕУ
СНБпШЁздШЛЖдЪ§ЕУ![]() ЃЌ
ЃЌ
Сю![]() ЕУ
ЕУ![]() Чв
Чв![]()
ИљОнЫљИјЭГМЦСПМАзюаЁГЫЙРМЦЙЋЪНгаЃЌ

![]() ЕУ
ЕУ![]() ЕУ
ЕУ![]()
ЫљЧѓ![]() Йигк
Йигк![]() ЕФЛиЙщЗНГЬЮЊ
ЕФЛиЙщЗНГЬЮЊ![]() ПЩжЊЃЌ
ПЩжЊЃЌ
ЃЈii)гЩЃЈi)ЃЌ![]() ЃЌдђ
ЃЌдђ![]()
гЩгХЕШЦЗжЪСПгыГпДчЕФБШ МД
МД![]()
Сю![]()
![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ШЁзюДѓжЕ
ШЁзюДѓжЕ
МДгХЕШЦЗЕФГпДч![]() ЃЌЪевц
ЃЌЪевц![]() ЕФдЄБЈжЕзюДѓ.
ЕФдЄБЈжЕзюДѓ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=Љ![]() sin2x+sinxcosx+
sin2x+sinxcosx+![]() ЃЌxЁЪ[0ЃЌ
ЃЌxЁЪ[0ЃЌ![]() ]
]
ЃЈ1ЃЉЧѓКЏЪ§fЃЈxЃЉЕФжЕгђЃЛ
ЃЈ2ЃЉШєfЃЈ![]() ЃЉ=
ЃЉ=![]() ЃЌІСЁЪЃЈ0ЃЌІаЃЉЃЌЧѓsinІСЕФжЕЃЎ
ЃЌІСЁЪЃЈ0ЃЌІаЃЉЃЌЧѓsinІСЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПДќзгРягаЭъШЋЯрЭЌЕФ3жЛКьЧђКЭ4жЛКкЧђЃЌНёДгДќзгРяЫцЛњШЁЧђ.
ЃЈЂёЃЉШєгаЗХЛиЕиШЁ3ДЮЃЌУПДЮШЁвЛИіЧђЃЌЧѓШЁГі2ИіКьЧђ1ИіКкЧђЕФИХТЪЃЛ
ЃЈЂђЃЉШєЮоЗХЛиЕиШЁ3ДЮЃЌУПДЮШЁвЛИіЧђЃЌШєШЁГіУПжЛКьЧђЕУ2ЗжЃЌШЁГіУПжЛКкЧђЕУ1ЗжЃЌЧѓЕУЗж![]() ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌФГЕиГіЭСЕФвЛжжЁАЖЄЁБЪЧгЩЫФЬѕЯпЖЮзщГЩЃЌЦфНсЙЙФмЪЙЫќШЮвтХзжСЫЎЦНУцКѓЃЌзмгавЛЖЫЫљдкЕФжБЯпЪњжБЯђЩЯЃЎВЂМЧзщГЩИУЁАЖЄЁБЕФЫФЬѕЕШГЄЕФЯпЖЮЙЋЙВЕуЮЊ![]() ЃЌЖЄМтЮЊ
ЃЌЖЄМтЮЊ![]() ЃЎ
ЃЎ

ЃЈ1ЃЉХаЖЯЫФУцЬх![]() ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЩш![]() ЃЌЕБ
ЃЌЕБ![]() дкЭЌвЛЫЎЦНУцФкЪБЃЌЧѓ
дкЭЌвЛЫЎЦНУцФкЪБЃЌЧѓ![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФДѓаЁЃЈНсЙћгУЗДШ§НЧКЏЪ§жЕБэЪОЃЉЃЛ
ЫљГЩНЧЕФДѓаЁЃЈНсЙћгУЗДШ§НЧКЏЪ§жЕБэЪОЃЉЃЛ
ЃЈ3ЃЉШєИУЁАЖЄЁБзХЕиКѓЕФЫФИіЯпЖЮИљОнашвЊПЩвдЕїНкгыЕзУцГЩНЧЕФДѓаЁЃЌЧвБЃГжШ§ИіЯпЖЮгыЕзУцГЩНЧЯрЭЌЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЮЪ
ЃЌЮЪ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() ЕФЬхЛ§зюДѓЃЌВЂЧѓГізюДѓжЕЃЎ
ЕФЬхЛ§зюДѓЃЌВЂЧѓГізюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЃЌКЏЪ§
ЃЌКЏЪ§![]() .
.
ЃЈ1ЃЉЕБ![]() ЪБЃЌНтВЛЕШЪН
ЪБЃЌНтВЛЕШЪН![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() ЕФНтМЏжаЧЁгавЛИідЊЫиЃЌЧѓ
ЕФНтМЏжаЧЁгавЛИідЊЫиЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЩш![]() ЃЌШєЖдШЮвт
ЃЌШєЖдШЮвт![]() ЃЌКЏЪ§
ЃЌКЏЪ§![]() дкЧјМф
дкЧјМф![]() ЩЯЕФзюДѓжЕгызюаЁжЕЕФВюВЛГЌЙ§1ЃЌЧѓ
ЩЯЕФзюДѓжЕгызюаЁжЕЕФВюВЛГЌЙ§1ЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОаЁЬтЙВ![]() ЗжЃЉ
ЗжЃЉ
Шє![]() Лђ
Лђ![]() ЃЌдђГЦ
ЃЌдђГЦ![]() ЮЊ
ЮЊ![]() КЭ
КЭ![]() ЕФвЛИі
ЕФвЛИі![]() ЮЛХХСаЃЌЖдгк
ЮЛХХСаЃЌЖдгк![]() ЃЌНЋХХСа
ЃЌНЋХХСа![]() МЧЮЊ
МЧЮЊ![]() ЃЌНЋХХСа
ЃЌНЋХХСа![]() МЧЮЊ
МЧЮЊ![]() ЃЌвРДЫРрЭЦЃЌжБжС
ЃЌвРДЫРрЭЦЃЌжБжС![]() ЃЌЖдгкХХСа
ЃЌЖдгкХХСа![]() КЭ
КЭ![]() ЃЌЫќУЧЖдгІЮЛжУЪ§зжЯрЭЌЕФИіЪ§МѕШЅЖдгІЮЛжУЪ§зжВЛЭЌЕФЪ§ЃЌНазі
ЃЌЫќУЧЖдгІЮЛжУЪ§зжЯрЭЌЕФИіЪ§МѕШЅЖдгІЮЛжУЪ§зжВЛЭЌЕФЪ§ЃЌНазі![]() КЭ
КЭ![]() ЕФЯрЙижЕЃЌМЧзї
ЕФЯрЙижЕЃЌМЧзї![]() ЃЌР§Шч
ЃЌР§Шч![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]() ЃЌШє
ЃЌШє![]() ЃЌдђГЦ
ЃЌдђГЦ![]() ЮЊзюМбХХСаЃЎ
ЮЊзюМбХХСаЃЎ
ЃЈЂёЃЉаДГіЫљгаЕФзюМбХХСа![]() ЃЎ
ЃЎ
ЃЈЂђЃЉжЄУїЃКВЛДцдкзюМбХХСа![]() ЃЎ
ЃЎ
ЃЈЂѓЃЉШєФГИі![]() ЃЈ
ЃЈ![]() ЪЧе§ећЪ§ЃЉЮЊзюМбХХСаЃЌЧѓХХСа
ЪЧе§ећЪ§ЃЉЮЊзюМбХХСаЃЌЧѓХХСа![]() жа
жа![]() ЕФИіЪ§ЃЎ
ЕФИіЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.
ЃЈ1ЃЉЕБ![]() ЪБЃЌШє
ЪБЃЌШє![]() дкЧјМф
дкЧјМф![]() ЩЯЕЅЕїЕнМѕЃЌЧѓaЕФШЁжЕЗЖЮЇЃЛ
ЩЯЕЅЕїЕнМѕЃЌЧѓaЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЧѓТњзуЯТСаЬѕМўЕФЫљгаЪЕЪ§Жд![]() ЃКЕБaЪЧећЪ§ЪБЃЌДцдк
ЃКЕБaЪЧећЪ§ЪБЃЌДцдк![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЪЧ
ЪЧ![]() ЕФзюДѓжЕЃЌ
ЕФзюДѓжЕЃЌ![]() ЪЧ
ЪЧ![]() ЕФзюаЁжЕЃЛ
ЕФзюаЁжЕЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаДГіЯТСаИїзщУќЬтЙЙГЩЕФЁА![]() Лђ
Лђ![]() ЁБЁЂЁА
ЁБЁЂЁА![]() Чв
Чв![]() ЁБвдМАЁАЗЧ
ЁБвдМАЁАЗЧ![]() ЁБаЮЪНЕФУќЬтЃЌВЂХаЖЯЫќУЧЕФецМйЃЎ
ЁБаЮЪНЕФУќЬтЃЌВЂХаЖЯЫќУЧЕФецМйЃЎ
(1)![]() ЃК
ЃК![]() ЪЧгаРэЪ§ЃЌ
ЪЧгаРэЪ§ЃЌ![]() ЃК
ЃК![]() ЪЧећЪ§ЃЛ
ЪЧећЪ§ЃЛ
(2)![]() ЃКВЛЕШЪН
ЃКВЛЕШЪН![]() ЕФНтМЏЪЧ
ЕФНтМЏЪЧ![]() ЃЌ
ЃЌ![]() ЃКВЛЕШЪН
ЃКВЛЕШЪН![]() ЕФНтМЏЪЧ
ЕФНтМЏЪЧ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮ![]() ЮЊе§ЗНаЮЃЌ
ЮЊе§ЗНаЮЃЌ![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.
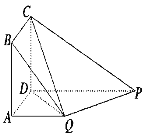
ЃЈ1ЃЉжЄУїЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓЖўУцНЧ![]() ЕФгрЯвжЕ.
ЕФгрЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com