
【题目】袋子里有完全相同的3只红球和4只黑球,今从袋子里随机取球.
(Ⅰ)若有放回地取3次,每次取一个球,求取出2个红球1个黑球的概率;
(Ⅱ)若无放回地取3次,每次取一个球,若取出每只红球得2分,取出每只黑球得1分,求得分![]() 的分布列和数学期望.
的分布列和数学期望.
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 为矩形,
为矩形,![]() ,
,![]() 均为等边三角形,
均为等边三角形,![]() ,
,![]() .
.
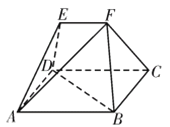
(1)过![]() 作截面与线段
作截面与线段![]() 交于点
交于点![]() ,使得
,使得![]() 平面
平面![]() ,试确定点
,试确定点![]() 的位置,并予以证明;
的位置,并予以证明;
(2)在(1)的条件下,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心在直线l:2x﹣y=0上,且与直线l1:x﹣y+1=0相切.
(Ⅰ)若圆C与圆x2+y2﹣2x﹣4y﹣76=0外切,试求圆C的半径;
(Ⅱ)满足已知条件的圆显然不只一个,但它们都与直线l1相切,我们称l1是这些圆的公切线.这些圆是否还有其他公切线?若有,求出公切线的方程,若没有,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型高端制造公司为响应《中国制造2025》中提出的坚持“创新驱动、质量为先、绿色发展、结构优化、人才为本”的基本方针,准备加大产品研发投资,下表是该公司2017年5~12月份研发费用(百万元)和产品销量(万台)的具体数据:

(1)根据数据可知![]() 与
与![]() 之间存在线性相关关系
之间存在线性相关关系
(i)求出![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() );
);
(ii)若2018年6月份研发投人为25百万元,根据所求的线性回归方程估计当月产品的销量;
(2)公司在2017年年终总结时准备从该年8~12月份这5个月中抽取3个月的数据进行重点分析,求没有抽到9月份数据的概率.
参考数据: ![]() ,
,![]() .
.
参考公式:对于一组数据![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: 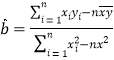 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=![]() sinωx+
sinωx+![]() cosωx(ω>0)的部分图象如图所示.
cosωx(ω>0)的部分图象如图所示.
(1)求ω的值;
(2)若x∈(-![]() ,
,![]() ),求f(x)的值域;
),求f(x)的值域;
(3)若方程3[f(x)]2-f(x)+m=0在x∈(-![]() ,
,![]() )内有解,求实数m的取值范围.
)内有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集为R,函数f(x)=lg(1﹣x)的定义域为集合A,集合B={x|x2﹣x﹣6>0}.
(Ⅰ)求A∪B;
(Ⅱ)若C={x|m﹣1<x<m+1},C(A∩(RB)),求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国互联网信息技术的发展,网络购物已经成为许多人消费的一种重要方式,某市为了了解本市市民的网络购物情况,特委托一家网络公示进行了网络问卷调查,并从参与调查的10000名网民中随机抽取了200人进行抽样分析,得到了下表所示数据:
经常进行网络购物 | 偶尔或从不进行网络购物 | 合计 | |
男性 | 50 | 50 | 100 |
女性 | 60 | 40 | 100 |
合计 | 110 | 90 | 200 |
(1)依据上述数据,能否在犯错误的概率不超过![]() 的前提下认为该市市民进行网络购物的情况与性别有关?
的前提下认为该市市民进行网络购物的情况与性别有关?
(2)现从所抽取的女性网民中利用分层抽样的方法再抽取![]() 人,从这
人,从这![]() 人中随机选出
人中随机选出![]() 人赠送网络优惠券,求出选出的
人赠送网络优惠券,求出选出的![]() 人中至少有两人是经常进行网络购物的概率;
人中至少有两人是经常进行网络购物的概率;
(3)将频率视为概率,从该市所有的参与调查的网民中随机抽取![]() 人赠送礼物,记经常进行网络购物的人数为
人赠送礼物,记经常进行网络购物的人数为![]() ,求
,求![]() 的期望和方差.
的期望和方差.
附:![]() ,其中
,其中![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸
与尺寸![]() 之间近似满足关系式
之间近似满足关系式![]() 为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间
为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品.现随机抽取6件合格产品,测得数据如下:
内时为优等品.现随机抽取6件合格产品,测得数据如下:
尺寸 | 38 | 48 | 58 | 68 | 78 | 88 |
质量 | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
质量与尺寸的比 | 0.442 | 0.392 | 0.367 | 0.329 | 0.308 | 0.290 |
(I)现从抽取的6件合格产品中再任选3件,记![]() 为取到优等品的件数,试求随机变量
为取到优等品的件数,试求随机变量![]() 的分布列和期望;
的分布列和期望;
(II)根据测得数据作了初步处理,得相关统计量的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(i)根据所给统计量,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(ii)已知优等品的收益![]() (单位:千元)与
(单位:千元)与![]() 的关系为
的关系为![]() ,则当优等品的尺寸
,则当优等品的尺寸![]() 为何值时,收益
为何值时,收益![]() 的预报值最大? (精确到0.1)
的预报值最大? (精确到0.1)
附:对于样本![]() , 其回归直线
, 其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
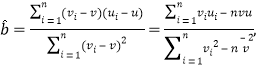
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 和等比数列
和等比数列![]() ,其中
,其中![]() 的公差不为0.设
的公差不为0.设![]() 是数列
是数列![]() 的前n项和.若
的前n项和.若![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前3项,且
的前3项,且![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)若数列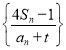 为等差数列,求实数t;
为等差数列,求实数t;
(3)构造数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,….若该数列前n项和
,….若该数列前n项和![]() ,求n的值.
,求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com