
【题目】已知圆C的圆心在直线l:2x﹣y=0上,且与直线l1:x﹣y+1=0相切.
(Ⅰ)若圆C与圆x2+y2﹣2x﹣4y﹣76=0外切,试求圆C的半径;
(Ⅱ)满足已知条件的圆显然不只一个,但它们都与直线l1相切,我们称l1是这些圆的公切线.这些圆是否还有其他公切线?若有,求出公切线的方程,若没有,说明理由.
【答案】(Ⅰ)![]() 1;(Ⅱ)还存在一条公切线,其方程为7x﹣y+5=0.
1;(Ⅱ)还存在一条公切线,其方程为7x﹣y+5=0.
【解析】
(I)设出圆![]() 的圆心坐标,利用圆心到直线
的圆心坐标,利用圆心到直线![]() 的距离表示半径,再根据两圆外切的条件列方程,解方程求得圆
的距离表示半径,再根据两圆外切的条件列方程,解方程求得圆![]() 的半径.
的半径.
(II)将另一条公切线的斜率分成存在和不存在两种情况进行分类讨论,结合圆心到两条公切线的距离相等列方程,由此求得另一条公切线的方程.
(Ⅰ)设圆C的圆心坐标为(a,2a),则半径r![]() ,
,
两圆的连心线长为![]() |a﹣1|
|a﹣1|![]() r,
r,
因为两圆外切,所以![]() r=r+9,∴r
r=r+9,∴r![]() 1;
1;
(Ⅱ)如果存在另一条切线,则它必过l与l1的交点(1,2),
①若斜率不存在,则直线方程为:x=1,圆心C到它的距离|a﹣1|=r![]() ,
,
由于方程需要对任意的a都成立,因此无解,所以它不是公切线,
②若斜率存在,设公切线方程为:y﹣2=k(x﹣1),
则d![]() r
r![]() 对任意的a都成立,
对任意的a都成立,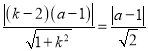 ,
,![]() ,两边平方并化简得k2﹣8k+7=0,解得k=1或k=7,
,两边平方并化简得k2﹣8k+7=0,解得k=1或k=7,
当k=1时,直线与l1重合,
当k=7时,直线方程为7x﹣y+5=0,
故还存在一条公切线,其方程为7x﹣y+5=0.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:
【题目】某校高一2班学生每周用于数学学习的时间![]() (单位:
(单位:![]() )与数学成绩
)与数学成绩![]() (单位:分)之间有如下数据:
(单位:分)之间有如下数据:
| 24 | 15 | 23 | 19 | 16 | 11 | 20 | 16 | 17 | 13 |
| 92 | 79 | 97 | 89 | 64 | 47 | 83 | 68 | 71 | 59 |
某同学每周用于数学学习的时间为18小时,试预测该生数学成绩.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划在办公大厅建一面长为![]() 米的玻璃幕墙.先等距安装
米的玻璃幕墙.先等距安装![]() 根立柱,然后在相邻的立柱之间安装一块与立柱等高的同种规格的玻璃.一根立柱的造价为6400元,一块长为
根立柱,然后在相邻的立柱之间安装一块与立柱等高的同种规格的玻璃.一根立柱的造价为6400元,一块长为![]() 米的玻璃造价为
米的玻璃造价为![]() 元.假设所有立柱的粗细都忽略不计,且不考虑其他因素,记总造价为
元.假设所有立柱的粗细都忽略不计,且不考虑其他因素,记总造价为![]() 元(总造价=立柱造价+玻璃造价).
元(总造价=立柱造价+玻璃造价).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,怎样设计能使总造价最低?
时,怎样设计能使总造价最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣![]() sin2x+sinxcosx+
sin2x+sinxcosx+![]() ,x∈[0,
,x∈[0,![]() ]
]
(1)求函数f(x)的值域;
(2)若f(![]() )=
)=![]() ,α∈(0,π),求sinα的值.
,α∈(0,π),求sinα的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的顶点在坐标原点,焦点F在x轴上,抛物线C上一点![]() 到焦点F的距离为
到焦点F的距离为![]() .
.
![]() Ⅰ
Ⅰ![]() 求抛物线C的标准方程;
求抛物线C的标准方程;
![]() Ⅱ
Ⅱ![]() 设点
设点![]() ,过点
,过点![]() 的直线l与抛物线C相交于A,B两点,记直线MA与直线MB的斜率分别为
的直线l与抛物线C相交于A,B两点,记直线MA与直线MB的斜率分别为![]() ,
,![]() ,证明:
,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有关命题的说法错误的是( )
A.若p∨q为假命题,则p、q均为假命题
B.“x=1”是“x2﹣3x+2=0”的充分不必要条件
C.命题“若x2﹣3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2﹣3x+2≠0”
D.对于命题p:x≥0,2x=3,则¬P:x<0,2x≠3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子里有完全相同的3只红球和4只黑球,今从袋子里随机取球.
(Ⅰ)若有放回地取3次,每次取一个球,求取出2个红球1个黑球的概率;
(Ⅱ)若无放回地取3次,每次取一个球,若取出每只红球得2分,取出每只黑球得1分,求得分![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,若
时,若![]() 在区间
在区间![]() 上单调递减,求a的取值范围;
上单调递减,求a的取值范围;
(2)求满足下列条件的所有实数对![]() :当a是整数时,存在
:当a是整数时,存在![]() ,使得
,使得![]() 是
是![]() 的最大值,
的最大值,![]() 是
是![]() 的最小值;
的最小值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com