
【题目】某公司计划在办公大厅建一面长为![]() 米的玻璃幕墙.先等距安装
米的玻璃幕墙.先等距安装![]() 根立柱,然后在相邻的立柱之间安装一块与立柱等高的同种规格的玻璃.一根立柱的造价为6400元,一块长为
根立柱,然后在相邻的立柱之间安装一块与立柱等高的同种规格的玻璃.一根立柱的造价为6400元,一块长为![]() 米的玻璃造价为
米的玻璃造价为![]() 元.假设所有立柱的粗细都忽略不计,且不考虑其他因素,记总造价为
元.假设所有立柱的粗细都忽略不计,且不考虑其他因素,记总造价为![]() 元(总造价=立柱造价+玻璃造价).
元(总造价=立柱造价+玻璃造价).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,怎样设计能使总造价最低?
时,怎样设计能使总造价最低?
科目:高中数学 来源: 题型:
【题目】在如图所示的多面体中,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,![]() 是
是![]() 的中点.
的中点.
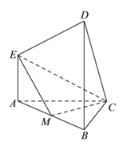
(1)求证:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成的二面角的正弦值;
所成的二面角的正弦值;
(3)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角是
所成的角是![]() . 若存在,指出点
. 若存在,指出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解男性家长和女性家长对高中学生成人礼仪式的接受程度,某中学团委以问卷形式调查了![]() 位家长,得到如下统计表:
位家长,得到如下统计表:

(1)据此样本,能否有![]() 的把握认为“接受程度”与家长性别有关?说明理由;
的把握认为“接受程度”与家长性别有关?说明理由;
(2)学校决定从男性家长中按分层抽样方法选出![]() 人参加今年的高中学生成人礼仪式,并从中选
人参加今年的高中学生成人礼仪式,并从中选![]() 人交流发言,设
人交流发言,设![]() 是发言人中持“赞成”态度的人数,求
是发言人中持“赞成”态度的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据
|
|
|
|
|
|
参考公式
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为正方形,侧棱
中,底面ABCD为正方形,侧棱![]() 底面ABCD,且
底面ABCD,且![]() ,E,F,H分别是线段PA,PD,AB的中点.
,E,F,H分别是线段PA,PD,AB的中点.
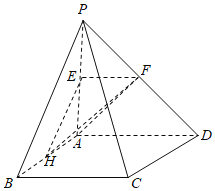
(1)求证:![]() 平面EFH;
平面EFH;
(2)求证:![]() 平面AHF;
平面AHF;
(3)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是( )
A. 若p∨q为假命题,则p∧q为假命题
B. 若a,b∈[0,1],则不等式a2+b2<![]() 成立的概率是
成立的概率是![]()
C. 命题“x∈R,使得x2+x+1<0”的否定是“x∈R,x2+x+1≥0”
D. 已知函数f(x)可导,则“f′(x0)=0”是“x0是函数f(x)的极值点”的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经销商销售某种产品,在一个销售季度内,每售出![]() 该产品获利润
该产品获利润![]() 元;未售出的产品,每
元;未售出的产品,每![]() 亏损
亏损![]() 元.根据以往的销售记录,得到一个销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了
元.根据以往的销售记录,得到一个销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了![]() 该产品.用
该产品.用![]() (单位:
(单位:![]() ,
,![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量,![]() (单位:元)表示下一个销售季度内经销该产品的利润.
(单位:元)表示下一个销售季度内经销该产品的利润.

(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)根据直方图估计利润![]() 不少于
不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥PABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD的中点,则
①棱AB与PD所在直线垂直;
②平面PBC与平面ABCD垂直;
③△PCD的面积大于△PAB的面积;
④直线AE与直线BF是异面直线.
以上结论正确的是________.(写出所有正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com