
【题目】已知等差数列![]() 和等比数列
和等比数列![]() ,其中
,其中![]() 的公差不为0.设
的公差不为0.设![]() 是数列
是数列![]() 的前n项和.若
的前n项和.若![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前3项,且
的前3项,且![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)若数列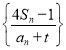 为等差数列,求实数t;
为等差数列,求实数t;
(3)构造数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,….若该数列前n项和
,….若该数列前n项和![]() ,求n的值.
,求n的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)41.
;(3)41.
【解析】
(1)设![]() 的公差
的公差![]() ,由
,由![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前3项,可得
的前3项,可得![]() 即
即![]() ,又
,又![]() 即
即![]() ,解得
,解得![]() ,
,![]() ,即可得出通项公式;
,即可得出通项公式;
(2)![]() ,可得
,可得![]() ,根据数列
,根据数列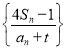 为等差数列,可得
为等差数列,可得![]() ,据此化简求解可得
,据此化简求解可得![]() 值;
值;
(3)设从![]() 到
到![]() 各项的和为
各项的和为![]() ,
,
则![]() ,进而可得
,进而可得 ,由
,由![]() ,
,![]() 得
得![]() ,进而可得该数列前36项的和,令
,进而可得该数列前36项的和,令![]() ,解方程可得
,解方程可得![]() 的值,进而得到
的值,进而得到![]() 的值.
的值.
(1)设![]() 的公差
的公差![]() ,
,![]()
![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前3项,且
的前3项,且![]() ,
,
![]()
![]() ,即
,即![]() ,
,![]() ,
,
解得![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,![]() ,公比
,公比![]() ,
,
![]()
![]() ;
;
(2)![]() ,
,
![]()
![]() ,
,
![]() 数列
数列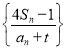 为等差数列,且
为等差数列,且![]() ,
,
![]() 该数列的前三项满足式子:
该数列的前三项满足式子:![]() ,即
,即![]() ,
,
解得![]() 或
或![]() ,经过验证满足题意;
,经过验证满足题意;
(3)由(1)可得:![]() ,数列
,数列![]() 的前n项和
的前n项和![]() ,
,
数列![]() 的前n项和
的前n项和![]() ,
,
设从![]() 到
到![]() 各项的和为
各项的和为![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]()
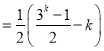 ,
,
![]()
 ,
,
![]()
![]() ,
,![]() ,
,
![]() 取
取![]() ,可得该数列前
,可得该数列前![]() 项的和为
项的和为![]() ,
,
令![]() ,解得
,解得![]() ,
,
因此![]() ,
,
即n的值为41.


科目:高中数学 来源: 题型:
【题目】袋子里有完全相同的3只红球和4只黑球,今从袋子里随机取球.
(Ⅰ)若有放回地取3次,每次取一个球,求取出2个红球1个黑球的概率;
(Ⅱ)若无放回地取3次,每次取一个球,若取出每只红球得2分,取出每只黑球得1分,求得分![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,若
时,若![]() 在区间
在区间![]() 上单调递减,求a的取值范围;
上单调递减,求a的取值范围;
(2)求满足下列条件的所有实数对![]() :当a是整数时,存在
:当a是整数时,存在![]() ,使得
,使得![]() 是
是![]() 的最大值,
的最大值,![]() 是
是![]() 的最小值;
的最小值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】写出下列各组命题构成的“![]() 或
或![]() ”、“
”、“![]() 且
且![]() ”以及“非
”以及“非![]() ”形式的命题,并判断它们的真假.
”形式的命题,并判断它们的真假.
(1)![]() :
:![]() 是有理数,
是有理数,![]() :
:![]() 是整数;
是整数;
(2)![]() :不等式
:不等式![]() 的解集是
的解集是![]() ,
,![]() :不等式
:不等式![]() 的解集是
的解集是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 (1)已知正数a,b满足a+b=1,求证:a2+b2≥![]() ;
;
(2)设a、b、c为△ABC的三条边,求证:a2+b2+c2<2(ab+bc+ca).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,圆
,圆![]() :
:![]() ,点
,点![]() 是圆
是圆![]() 上一动点,线段
上一动点,线段![]() 的垂直平分线与
的垂直平分线与![]() 交于点
交于点![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)曲线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,直线
,直线![]() 过点
过点![]() 且垂直于
且垂直于![]() 轴,点
轴,点![]() 在直线
在直线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,若
上,若![]() ,试判断直线
,试判断直线![]() 与曲线
与曲线![]() 的交点的个数.
的交点的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com