
【题目】 (1)已知正数a,b满足a+b=1,求证:a2+b2≥![]() ;
;
(2)设a、b、c为△ABC的三条边,求证:a2+b2+c2<2(ab+bc+ca).
【答案】(1)见解析(2)见解析
【解析】
试题(1)利用配方将a2+b2化为1-2ab,再根据基本不等式证不等式(2)根据三角形两边之和大于第三边得a+c>b,即得ab+bc>b2,同理可得bc+ca>c2 ,ab+ca>a2,三式相加即得结论
试题解析:证明:(1)a2+b2=(a+b)2-2ab=1-2ab≥1-2×![]() =1-
=1-![]() =
=![]() .
.
(2)因为a,b,c是△ABC的三边,不妨设a≥b≥c>0,则a>b-c≥0,b>a-c≥0,c>a-b≥0.平方得:
a2>b2+c2-2bc,b2>a2+c2-2ac,c2>a2+b2-2ab,
三式相加得:0>a2+b2+c2-2bc-2ac-2ab.
所以2ab+2bc+2ac>a2+b2+c2,
即a2+b2+c2<2(ab+bc+ca).


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】已知全集为R,函数f(x)=lg(1﹣x)的定义域为集合A,集合B={x|x2﹣x﹣6>0}.
(Ⅰ)求A∪B;
(Ⅱ)若C={x|m﹣1<x<m+1},C(A∩(RB)),求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知从![]() 地去
地去![]() 地有①或②两条路可走,并且汽车走路①堵车的概率为
地有①或②两条路可走,并且汽车走路①堵车的概率为![]() ,汽车走路②堵车的概率为
,汽车走路②堵车的概率为![]() ,若现在有两辆汽车走路①,有一辆汽车走路②,且这三辆车是否堵车相互之间没有影响,
,若现在有两辆汽车走路①,有一辆汽车走路②,且这三辆车是否堵车相互之间没有影响,
(1)若这三辆汽车中恰有一辆汽车被堵的概率为![]() ,求走路②堵车的概率;
,求走路②堵车的概率;
(2)在(1)的条件下,求这三辆汽车中被堵车辆的辆数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 和等比数列
和等比数列![]() ,其中
,其中![]() 的公差不为0.设
的公差不为0.设![]() 是数列
是数列![]() 的前n项和.若
的前n项和.若![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前3项,且
的前3项,且![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)若数列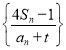 为等差数列,求实数t;
为等差数列,求实数t;
(3)构造数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,….若该数列前n项和
,….若该数列前n项和![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品,每售出一吨可获利![]() 万元,每积压一吨则亏损
万元,每积压一吨则亏损![]() 万元.某经销商统计出过去
万元.某经销商统计出过去![]() 年里市场年需求量的频数分布表如下表所示.
年里市场年需求量的频数分布表如下表所示.
年需求量(吨) |
|
|
|
|
|
年数 |
|
|
|
|
|
(1)求过去![]() 年年需求量的平均值;(每个区间的年需求量用中间值代替)
年年需求量的平均值;(每个区间的年需求量用中间值代替)
(2)今年该经销商欲进货![]() 吨,以
吨,以![]() (单位:吨,
(单位:吨,![]() )表示今年的年需求量,以
)表示今年的年需求量,以![]() (单位:万元)表示今年销售的利润,试将
(单位:万元)表示今年销售的利润,试将![]() 表示
表示![]() 的函数解析式,并求今年的年利润不少于
的函数解析式,并求今年的年利润不少于![]() 万元的概率.
万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(-2,2),函数g(x)=f(x-1)+f(3-2x).
(1)求函数g(x)的定义域;
(2)若f(x)是奇函数,且在定义域上单调递减,求不等式g(x)≤0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,
, ![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 把![]() 上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
B. 把![]() 上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
C. 把曲线![]() 向右平移
向右平移![]() 个单位长度,再把得到的曲线上各点横坐标缩短到原来的
个单位长度,再把得到的曲线上各点横坐标缩短到原来的![]() ,纵坐标不变,得到曲线
,纵坐标不变,得到曲线![]()
D. 把曲线![]() 向右平移
向右平移![]() 个单位长度,再把得到的曲线上各点横坐标缩短到原来的
个单位长度,再把得到的曲线上各点横坐标缩短到原来的![]() ,纵坐标不变,得到曲线
,纵坐标不变,得到曲线![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com