
【题目】已知函数![]() .
.
(1)判断![]() 的单调性,并说明理由;
的单调性,并说明理由;
(2)判断![]() 的奇偶性,并用定义证明;
的奇偶性,并用定义证明;
(3)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)增函数,理由见解析 (2)奇函数,证明见解析 (3)![]()
【解析】
(1)利用函数单调性的定义即可得证.
(2)首先判断定义域关于原点对称,利用函数奇偶性定义即可得证.
(3)由(1)(2)以及分离参数法将不等式转化为![]() 对任意
对任意![]() 恒成立,令
恒成立,令![]() ,求
,求![]() 的最大值即可.
的最大值即可.
解:(1)![]() 是定义域
是定义域![]() 上的增函数.
上的增函数.
设任意的![]() ,且
,且![]() ,则
,则
![]() ,
,
因为![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]()
即![]() ,所以
,所以![]() 是定义域
是定义域![]() 上的增函数.
上的增函数.
(2)![]() 是奇函数.
是奇函数.
证明:因为![]() ,定义域
,定义域![]() 关于原点对称
关于原点对称
所以对任意![]() ,都有
,都有![]()
所以![]() 是奇函数.
是奇函数.
(3)由(2)知![]() 为
为![]() 上的奇函数,所以不等式
上的奇函数,所以不等式![]() 对任意
对任意![]() 恒成立,等价于
恒成立,等价于![]() 对任意
对任意![]() 恒成立.
恒成立.
又由(1)知,![]() 在定义域
在定义域![]() 上单调递增,
上单调递增,
得![]() 对任意
对任意![]() 恒成立即
恒成立即![]() 对任意
对任意![]() 恒成立.
恒成立.
设![]() ,
,
则![]() ,故
,故![]() 在
在![]() 上的最大值为
上的最大值为![]() ,
,
所以实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】 (1)已知正数a,b满足a+b=1,求证:a2+b2≥![]() ;
;
(2)设a、b、c为△ABC的三条边,求证:a2+b2+c2<2(ab+bc+ca).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在[50,100]内,发布成绩使用等级制.各等级划分标准见图表.规定:A,B,C三级为合格等级,D为不合格等级.
分数 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | A | B | C | D |
为了解该校高一年级学生身体素质情况,从中抽取了n名学生的原始成绩作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图①所示,样本中原始成绩在80分及以上的所有数据的茎叶图如图②所示.
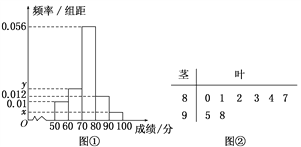
(1)求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
(2)在选取的样本中,从成绩为A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生的成绩是A等级的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第![]() 年需要付出设备的维修和工人工资等费用
年需要付出设备的维修和工人工资等费用![]() 的信息如下图.
的信息如下图.
(1)求![]() ;
;
(2)引进这种设备后,从第几年开始该公司能够获利?
(3)这种设备使用多少年,该公司的年平均获利最大?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种产品的年固定成本为200万元,每生产![]() 千件,需另投入成本为
千件,需另投入成本为![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时,![]() (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于一个具有正南正北、正东正西方向规则布局的城镇街道,从一点到另一点的距离是在南北方向上行进的距离加上在东西方向上行进的距离,这种距离即“曼哈顿距离”,也叫“出租车距离”.对于平面直角坐标系中的点![]() 和
和![]() ,两点间的“曼哈顿距离”
,两点间的“曼哈顿距离”![]() .
.

(1)如图,若![]() 为坐标原点,
为坐标原点,![]() ,
,![]() 两点坐标分别为
两点坐标分别为![]() 和
和![]() ,求
,求![]() ,
,![]() ,
,![]() ;
;
(2)若点![]() 满足
满足![]() ,试在图中画出点
,试在图中画出点![]() 的轨迹,并求该轨迹所围成图形的面积;
的轨迹,并求该轨迹所围成图形的面积;
(3)已知函数![]() ,试在
,试在![]() 图象上找一点
图象上找一点![]() ,使得
,使得![]() 最小,并求出此时点
最小,并求出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com