
已知函数
(1)当 时,求函数
时,求函数 的最小值和最大值
的最小值和最大值
(2)设三角形角 的对边分别为
的对边分别为 且
且 ,
,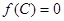 ,若
,若 ,求
,求 的值.
的值.
(1)最小值为 ,最大值为0;(2)
,最大值为0;(2) .
.
解析试题分析:(1)先通过三角函数的恒等变形化 的形式后再解答;一般地,涉及三角函数的值域问题,多数情况下要将其变形为
的形式后再解答;一般地,涉及三角函数的值域问题,多数情况下要将其变形为 后,再利用三角函数的性质解答,也有部分题目,可转化为角的某个三角函数,然后用换元法转化为非三角函数问题;(2)由
后,再利用三角函数的性质解答,也有部分题目,可转化为角的某个三角函数,然后用换元法转化为非三角函数问题;(2)由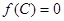 先求出
先求出 ,再利用正弦定理求出
,再利用正弦定理求出 ,再利用余弦定理则可求出
,再利用余弦定理则可求出 .在三角形中求角或边,通常对条件进行“统一”,统一为边或统一为角,主要的工具是正弦定理和余弦定理,同时不要忘记了三角形内角和定理.
.在三角形中求角或边,通常对条件进行“统一”,统一为边或统一为角,主要的工具是正弦定理和余弦定理,同时不要忘记了三角形内角和定理.
试题解析:(1)
 ,因为
,因为  ,
, ,所以当
,所以当 时,
时, 取得最小值
取得最小值 ,当
,当 时,
时, 取得最大值0 6分
取得最大值0 6分
(2)由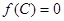 ,得
,得 ,又
,又 为三角形内角,所以
为三角形内角,所以 ,所以
,所以 ,由正弦定理结合
,由正弦定理结合 得,
得, ,再由余弦定理
,再由余弦定理 得,
得,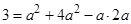 ,解得
,解得 ,所以
,所以 13分
13分
考点:三角函数性质、正弦定理、余弦定理.


科目:高中数学 来源: 题型:解答题
(本小题满分12分)如图,在△ABC中,∠ABC=90°,AB= ,BC=1,P为△ABC内一点,∠BPC=90°
,BC=1,P为△ABC内一点,∠BPC=90°
(1)若PB= ,求PA;
,求PA;
(2)若∠APB=150°,求tan∠PBA
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,有两座建筑物AB和CD都在河的对岸(不知 道它们的高度,且不能到达对岸),某人想测量两 座建筑物尖顶A、C之间的距离,但只有卷尺和测 角仪两种工具.若此人在地面上选一条基线EF,用 卷尺测得EF的长度为a,并用测角仪测量了一些角度: ,
, ,
, ,
, ,
, 请你用文字和公式写出计算A、C之间距离的步骤和结果.
请你用文字和公式写出计算A、C之间距离的步骤和结果.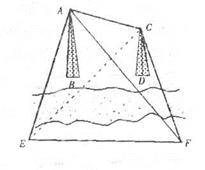
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com