
在△ABC中,若 .
.
(Ⅰ)判断△ABC的形状;
(Ⅱ)在上述△ABC中,若角C的对边 ,求该三角形内切圆半径的取值范围。
,求该三角形内切圆半径的取值范围。
(Ⅰ)直角三角形;(Ⅱ)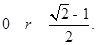
解析试题分析:(Ⅰ)先利用正弦定理和余弦定理把条件中关于角的等式转化为关于边的等式,再整理化简,通过最终的等式可以判断三角形的形状.
(Ⅱ)利用(Ⅰ)的结果和切线的性质把内切圆的半径用三角形的三条边表示出来,再把三角边转化为角的形式,从而把问题转化求三角函数的值域问题.
试题分析:(Ⅰ)根据正弦定理,原式可化为: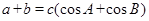 ,
,
再由余弦定理,上式可化为: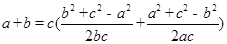 ,
,
即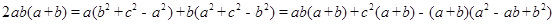
消去 整理得:
整理得: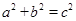 ,所以
,所以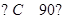 即△ABC为直角三角形.
即△ABC为直角三角形.
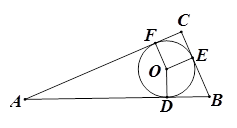
(Ⅱ)如图,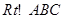 中,
中,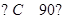 ,
,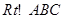 的内切圆
的内切圆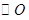 分别与边
分别与边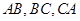 相切与点
相切与点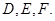
由切线长定理知: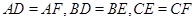
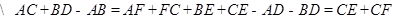
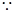 四边形
四边形 中,
中, 且
且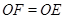
四边形为正方形,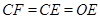
 的半径
的半径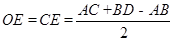
若设内切圆半径为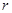 ,则
,则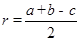 .
.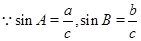 且
且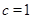 ,
,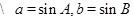 ,
,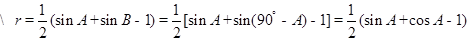
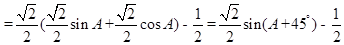
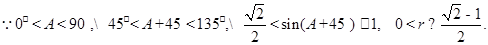
考点:1.正弦定理和余弦定理的应用;2.直角三角形内切圆的性质;3.三角恒等变换;4.三角函数的值域.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:解答题
已知向量 ,
, ,(
,( ,且
,且 为常数),设函数
为常数),设函数 ,若
,若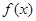 的最大值为1.
的最大值为1.
(1)求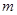 的值,并求
的值,并求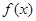 的单调递增区间;
的单调递增区间;
(2)在 中,角
中,角 、
、 、
、 的对边
的对边 、
、 、
、 ,若
,若 ,且
,且 ,试判断三角形的形状.
,试判断三角形的形状.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com