
(本小题满分14分)
已知函数 为常数,数列
为常数,数列 满足:
满足: ,
, ,
, .
.
(1)当 时,求数列
时,求数列 的通项公式;
的通项公式;
(2)在(1)的条件下,证明对 有:
有: ;
;
(3)若 ,且对
,且对 ,有
,有 ,证明:
,证明: .
.
(1) ,
,
(2)可以用裂项法求和进而证明也可以用数学归纳法证明
(3)可以用基本不等式证明也可以用导数证明,还可以利用数列的单调性证明
解析试题分析:(1)当 时,
时, ,
,
两边取倒数,得 , ……2分
, ……2分
故数列 是以
是以 为首项,为公差的等差数列,
为首项,为公差的等差数列,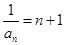 ,
, ,
, . ……4分
. ……4分
(2)证法1:由(1)知 ,故对
,故对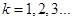

 ……6分
……6分
所以
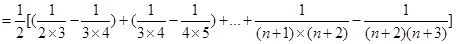

 . ……9分
. ……9分
[证法2:①当n=1时,等式左边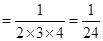 ,等式右边
,等式右边 ,左边=右边,等式成立; ……5分
,左边=右边,等式成立; ……5分
②假设当 时等式成立,
时等式成立,
即 ,
,
则当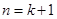 时
时


这就是说当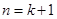 时,等式成立, ……8分
时,等式成立, ……8分
综①②知对于 有:
有: . ……9分】
. ……9分】
(3)当 时,
时,
则 , ……10分
, ……10分
∵ ,
,
∴ ……11分
……11分


 . ……13分
. ……13分
∵ 与
与 不能同时成立,∴上式“=”不成立,
不能同时成立,∴上式“=”不成立,
即对 ,
, . ……14分
. ……14分
【证法二:当 时,
时, ,
,
则 ……10分
……10分
又



 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:解答题
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:
①sin213°+cos217°-sin 13°cos 17°;
②sin215°+cos215°-sin 15°cos 15°;
③sin218°+cos212°-sin 18°cos 12°;
④sin2(-18°)+cos248°-sin(-18°)cos 48°;
⑤sin2(-25°)+cos255°-sin(-25°)cos 55°.
(1)试从上述五个式子中选择一个,求出这个常数;
(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com