
在直角坐标系xOy中,以O为极点,x轴非负半轴为极轴建立极坐标系,曲线C的极坐标方程为ρcos(θ-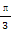 )=1,M,N分别为C与x轴,y轴的交点.
)=1,M,N分别为C与x轴,y轴的交点.
(1)写出C的直角坐标方程,并求M,N的极坐标.
(2)设MN的中点为P,求直线OP的极坐标方程.
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:填空题
某毕业生参加人才招聘会,分别向甲、乙、丙三个公司投递了个人简历.假定该毕业生得到甲公司面试的概率为 ,得到乙、丙两公司面试的概率均为p,且三个公司是否让其面试是相互独立的.记X为该毕业生得到面试的公司个数.若P(X=0)=
,得到乙、丙两公司面试的概率均为p,且三个公司是否让其面试是相互独立的.记X为该毕业生得到面试的公司个数.若P(X=0)=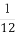 ,则随机变量X的数学期望E(X)= .
,则随机变量X的数学期望E(X)= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十三第十章第十节练习卷(解析版) 题型:解答题
某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组 数 | 分 组 | 低碳族的人数 | 占本组的频率 |
第一组 | [25,30) | 120 | 0.6 |
第二组 | [30,35) | 195 | p |
第三组 | [35,40) | 100 | 0.5 |
第四组 | [40,45) | a | 0.4 |
第五组 | [45,50) | 30 | 0.3 |
第六组 | [50,55] | 15 | 0.3 |
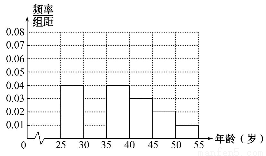
(1)补全频率分布直方图并求n,a,p的值.
(2)为调查该地区的年龄与生活习惯和是否符合低碳观念有无关系,调查组按40岁以下为青年,40岁以上(含40岁)为老年分成两组,请你先完成下面2×2列联表,并回答是否有99%的把握认为该地区的生活习惯是否符合低碳观念与人的年龄有关.
参考公式:χ2=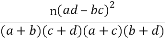
P(χ2≥x0) | 0.050 | 0.010 | 0.001 |
x0 | 3.841 | 6.635 | 10.828 |
年龄组
是否低碳族 | 青 年 | 老 年 | 总 计 |
低碳族 |
|
|
|
非低碳族 |
|
|
|
总计 |
|
|
|
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十三第十章第十节练习卷(解析版) 题型:选择题
在调查学生数学成绩与物理成绩之间的关系时,得到如下数据(人数):
| 物理 成绩好 | 物理 成绩不好 | 合计 |
数学成绩好 | 62 | 23 | 85 |
数学成绩不好 | 28 | 22 | 50 |
合计 | 90 | 45 | 135 |
那么有把握认为数学成绩与物理成绩之间有关的百分比为( )
(A)25% (B)75% (C)95% (D)99%
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十七选修4-4第一节练习卷(解析版) 题型:解答题
已知曲线C:ρsin(θ+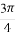 )=
)=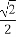 ,曲线P:ρ2-4ρcosθ+3=0,
,曲线P:ρ2-4ρcosθ+3=0,
(1)求曲线C,P的直角坐标方程.
(2)设曲线C和曲线P的交点为A,B,求|AB|.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:解答题
某市职教中心组织厨师技能大赛,大赛依次设基本功(初赛)、面点制作(复赛)、热菜烹制(决赛)三个轮次的比赛,已知某选手通过初赛、复赛、决赛的概率分别是 ,
, ,
, 且各轮次通过与否相互独立.
且各轮次通过与否相互独立.
(1)设该选手参赛的轮次为ξ,求ξ的分布列.
(2)对于(1)中的ξ,设“函数f(x)=3sin π(x∈R)是偶函数”为事件D,求事件D发生的概率.
π(x∈R)是偶函数”为事件D,求事件D发生的概率.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知向量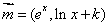 ,
,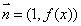 ,
,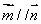 (
(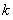 为常数,
为常数, 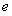 是自然对数的底数),曲线
是自然对数的底数),曲线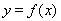 在点
在点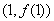 处的切线与
处的切线与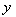 轴垂直,
轴垂直,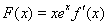 .
.
(Ⅰ)求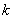 的值及
的值及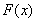 的单调区间;
的单调区间;
(Ⅱ)已知函数 (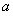 为正实数),若对于任意
为正实数),若对于任意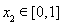 ,总存在
,总存在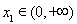 , 使得
, 使得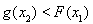 ,求实数
,求实数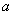 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年广东省广州市毕业班综合测试一理科数学试卷(解析版) 题型:解答题
已知函数 的图象经过点
的图象经过点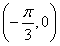 .
.
(1)求实数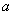 的值;
的值;
(2)设 ,求函数
,求函数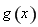 的最小正周期与单调递增区间.
的最小正周期与单调递增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com