
【题目】已知函数f(x)= ![]() ﹣m(lnx+
﹣m(lnx+ ![]() )(m为实数,e=2.71828…是自然对数的底数). (Ⅰ)当m>1时,讨论f(x)的单调性;
)(m为实数,e=2.71828…是自然对数的底数). (Ⅰ)当m>1时,讨论f(x)的单调性;
(Ⅱ)若g(x)=x2f′(x)﹣xex在( ![]() ,3)内有两个零点,求实数m的取值范围.
,3)内有两个零点,求实数m的取值范围.
(Ⅲ)当m=1时,证明:xf(x)+xlnx+1>x+ ![]() .
.
【答案】解:(Ⅰ)函数的定义域为(0,+∞), ![]() =
= ![]() . ∵m>1,令f′(x)=0,可得x=1,或x=lnm
. ∵m>1,令f′(x)=0,可得x=1,或x=lnm
①当m=e时,f′(x)≥0在(0,+∞)恒成立,∴此时f(x)在(0,+∞)递增;
②当m>e时,x∈(0,1)时,f′(x)>0,x∈(1,lnm)时,f′(x)<0,x∈(lnm,+∞)时,f′(x)>0
此时f(x)在(lnm,+∞),(0,1)递增,在(1,lnm)递减.
③当1<m<e时,x∈(0,lnm)时,f′(x)>0,x∈(lnm,1)时,f′(x)<0,x∈(1,+∞)时,f′(x)>0
此时f(x)在(1,+∞),(0,lnm)递增,在(lnm,1)递减.
(Ⅱ)g(x)=x2f′(x)﹣xex=﹣ex﹣m(x﹣1)在( ![]() ,3)内有两个零点,
,3)内有两个零点,
方程﹣ex﹣m(x﹣1)=0在( ![]() ,3)内有两个实根,
,3)内有两个实根,
即m=﹣ ![]() 在(
在( ![]() ,3)内有两个实根,
,3)内有两个实根,
令h(x)=﹣ ![]() ,h′(x)=
,h′(x)= ![]() =0,可得x=2,
=0,可得x=2,
x ![]() 时,h′(x)>0,x∈(2,3)时,h′(x)<0,
时,h′(x)>0,x∈(2,3)时,h′(x)<0,
∴h(x)在( ![]() )递增,在(2,3),递减,
)递增,在(2,3),递减,
要使g(x)=x2f′(x)﹣xex在( ![]() ,3)内有两个零点,则
,3)内有两个零点,则 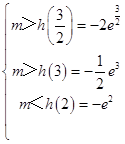
可得﹣ ![]() <m<﹣e2 , ∴实数m的取值范围为(﹣
<m<﹣e2 , ∴实数m的取值范围为(﹣ ![]() ,﹣e2).
,﹣e2).
(Ⅲ)证明:当m=1时,要证xf(x)+xlnx+1>x+ ![]() .
.
只证x( ![]() ﹣lnx﹣
﹣lnx﹣ ![]() )+xlnx+1>x+
)+xlnx+1>x+ ![]() 在(0,+∞)恒成立.
在(0,+∞)恒成立.
只证 ![]() ,易得ex>x+1在(0,+∞)恒成立,
,易得ex>x+1在(0,+∞)恒成立,
故只需证1> ![]() ,即证x>ln(x+1),
,即证x>ln(x+1),
令F(x)=x﹣ln(x+1),F′(x)=1﹣ ![]() >0,故F(x)在(0,+∞)递增,而F(0)=0
>0,故F(x)在(0,+∞)递增,而F(0)=0
∵F(x)>0在(0,+∞)恒成立.
∴xf(x)+xlnx+1>x+ ![]() 成立.
成立.
【解析】(Ⅰ)函数的定义域为(0,+∞), ![]() =
= ![]() .令f′(x)=0,可得x=1,或x=lnm 分①m=e,②m>e,③1<m<e分类讨论其单调性;(Ⅱ)g(x)=x2f′(x)﹣xex=﹣ex﹣m(x﹣1)在(
.令f′(x)=0,可得x=1,或x=lnm 分①m=e,②m>e,③1<m<e分类讨论其单调性;(Ⅱ)g(x)=x2f′(x)﹣xex=﹣ex﹣m(x﹣1)在( ![]() ,3)内有两个零点,
,3)内有两个零点,
方程﹣ex﹣m(x﹣1)=0在( ![]() ,3)内有两个实根,
,3)内有两个实根,
即m=﹣ ![]() 在(
在( ![]() ,3)内有两个实根,
,3)内有两个实根,
令h(x)=﹣ ![]() ,可得h(x)在(
,可得h(x)在( ![]() )递增,在(2,3),递减,
)递增,在(2,3),递减,
要使g(x)=x2f′(x)﹣xex在( ![]() ,3)内有两个零点,则
,3)内有两个零点,则 
可得实数m的取值范围为(﹣ ![]() ,﹣e2).(Ⅲ)当m=1时,要证xf(x)+xlnx+1>x+
,﹣e2).(Ⅲ)当m=1时,要证xf(x)+xlnx+1>x+ ![]() .只证x(
.只证x( ![]() ﹣lnx﹣
﹣lnx﹣ ![]() )+xlnx+1>x+
)+xlnx+1>x+ ![]() 在(0,+∞)恒成立.
在(0,+∞)恒成立.
只证 ![]() ,易得ex>x+1在(0,+∞)恒成立,
,易得ex>x+1在(0,+∞)恒成立,
故只需证1> ![]() ,即证x>ln(x+1)即可,
,即证x>ln(x+1)即可,
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】已知![]() .
.
(1)求函数![]() 的最小正周期和对称轴方程;
的最小正周期和对称轴方程;
(2)若![]() ,求
,求![]() 的值域.
的值域.
【答案】(1)对称轴为![]() ,最小正周期
,最小正周期![]() ;(2)
;(2)![]()
【解析】
(1)利用正余弦的二倍角公式和辅助角公式将函数解析式进行化简得到![]() ,由周期公式和对称轴公式可得答案;(2)由x的范围得到
,由周期公式和对称轴公式可得答案;(2)由x的范围得到![]() ,由正弦函数的性质即可得到值域.
,由正弦函数的性质即可得到值域.
(1)![]()
![]()
令![]() ,则
,则
![]() 的对称轴为
的对称轴为![]() ,最小正周期
,最小正周期![]() ;
;
(2)当![]() 时,
时,![]() ,
,
因为![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
在![]() 取最大值,在
取最大值,在![]() 取最小值,
取最小值,
所以![]() ,
,
所以![]() .
.
【点睛】
本题考查正弦函数图像的性质,考查周期性,对称性,函数值域的求法,考查二倍角公式以及辅助角公式的应用,属于基础题.
【题型】解答题
【结束】
21
【题目】已知等比数列![]() 的前
的前![]() 项和为
项和为![]() ,公比
,公比![]() ,
,![]() ,
,![]() .
.
(1)求等比数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求
,求![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(Ⅰ)如表所示是某市最近5年个人年平均收入表节选.求y关于x的回归直线方程,并估计第6年该市的个人年平均收入(保留三位有效数字).
年份x | 1 | 2 | 3 | 4 | 5 |
收入y(千元) | 21 | 24 | 27 | 29 | 31 |
其中![]() ,
,![]() ,
,![]() 附1:
附1:![]() =
= ![]() ,
,![]() =
=![]() ﹣
﹣![]()
![]()
(Ⅱ)下表是从调查某行业个人平均收入与接受专业培训时间关系得到2×2列联表:
受培时间一年以上 | 受培时间不足一年 | 总计 | |
收入不低于平均值 | 60 | 20 | |
收入低于平均值 | 10 | 20 | |
总计 | 100 |
完成上表,并回答:能否在犯错概率不超过0.05的前提下认为“收入与接受培训时间有关系”.
附2:
P(K2≥k0) | 0.50 | 0.40 | 0.10 | 0.05 | 0.01 | 0.005 |
k0 | 0.455 | 0.708 | 2.706 | 3.841 | 6.635 | 7.879 |
附3:
K2=![]() .(n=a+b+c+d)
.(n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四张卡片,分别写有“瓷、都、文、明”四个字,有放回地从中任取一张卡片,将三次抽取后“瓷”“都”两个字都取到记为事件![]() ,用随机模拟的方法估计事件
,用随机模拟的方法估计事件![]() 发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
232 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估计事件![]() 发生的概率为( )
发生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增大,下表是该地一农业银行连续五年的储蓄存款(年底余额),如下表:

为了研究方便,工作人员将上表的数据进行了处理,![]() ,得到下表:
,得到下表:

(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(3)用所求回归方程预测,到2020年底,该地储蓄存款额大约可达多少?
(附:线性回归方程:![]() ,
,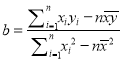 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P—ABC中,△PBC为等边三角形,点O为BC的中点,AC⊥PB,平面PBC⊥平面ABC.

(1)求直线PB和平面ABC所成的角的大小;
(2)求证:平面PAC⊥平面PBC;
(3)已知E为PO的中点,F是AB上的点,AF=![]() AB.若EF∥平面PAC,求
AB.若EF∥平面PAC,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣x3与g(x)=x3﹣ax的图象上存在关于x轴的对称点,则实数a的取值范围为( )
A.(﹣∞,e)
B.(﹣∞,e]
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现在,很多人都喜欢骑“共享单车”,但也有很多市民并不认可.为了调查人们对这种交通方式的认可度,某同学从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20名市民,得到了一个市民是否认可的样本,具体数据如下![]() 列联表:
列联表:

附:![]() ,
,![]() .
.

根据表中的数据,下列说法中,正确的是( )
A. 没有95% 以上的把握认为“是否认可与城市的拥堵情况有关”
B. 有99% 以上的把握认为“是否认可与城市的拥堵情况有关”
C. 可以在犯错误的概率不超过0.01的前提下认为“是否认可与城市的拥堵情况有关”
D. 可以在犯错误的概率不超过0.025的前提下认为“是否认可与城市的拥堵情况有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数![]() 的图象沿
的图象沿![]() 轴向左平移
轴向左平移![]() 个单位,纵坐标伸长到原来的2倍(横坐标不变)后得到函数
个单位,纵坐标伸长到原来的2倍(横坐标不变)后得到函数![]() 的图象,对于函数
的图象,对于函数![]() 有以下四个判断:
有以下四个判断:
①该函数的解析式为;![]() ;
;
②该函数图象关于点![]() 对称;
对称;
③该函数在![]() [,上是增函数;
[,上是增函数;
④函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,则
,则![]() .
.
其中,正确判断的序号是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com