
 如图,在△ABC中,已知CA=1,CB=2,∠ACB=60°.
如图,在△ABC中,已知CA=1,CB=2,∠ACB=60°.分析 (1)利用余弦定理求出AB的长即得|$\overrightarrow{AB}$|;
(2)①λ=$\frac{1}{2}$时,D、E分别是BC,AB的中点,求出$\overrightarrow{AE}$、$\overrightarrow{CD}$的数量积即可;
②假设存在非零实数λ,使得$\overrightarrow{AE}$⊥$\overrightarrow{CD}$,利用$\overrightarrow{CB}$、$\overrightarrow{CA}$分别表示出$\overrightarrow{CD}$和$\overrightarrow{AE}$,
求出$\overrightarrow{AE}$•$\overrightarrow{CD}$=0时的λ值即可.
解答 解:(1)△ABC中,CA=1,CB=2,∠ACB=60°,
由余弦定理得,
AB2=CA2+CB2-2CA•CB•cos∠ACB
=12+22-2×1×2×cos60°
=3,
∴AB=$\sqrt{3}$,即|$\overrightarrow{AB}$|=$\sqrt{3}$;
(2)①λ=$\frac{1}{2}$时,$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{AB}$,$\overrightarrow{BE}$=$\frac{1}{2}$$\overrightarrow{BC}$,
∴D、E分别是BC,AB的中点,
∴$\overrightarrow{AE}$=$\overrightarrow{AC}$+$\overrightarrow{CE}$=$\overrightarrow{AC}$+$\frac{1}{2}$$\overrightarrow{CB}$,
$\overrightarrow{CD}$=$\frac{1}{2}$($\overrightarrow{CA}$+$\overrightarrow{CB}$),
∴$\overrightarrow{AE}$•$\overrightarrow{CD}$=($\overrightarrow{AC}$+$\frac{1}{2}$$\overrightarrow{CB}$)•$\frac{1}{2}$($\overrightarrow{CA}$+$\overrightarrow{CB}$)
=$\frac{1}{2}$$\overrightarrow{AC}$•$\overrightarrow{CA}$+$\frac{1}{2}$$\overrightarrow{AC}$•$\overrightarrow{CB}$+$\frac{1}{4}$$\overrightarrow{CB}$•$\overrightarrow{CA}$+$\frac{1}{4}$${\overrightarrow{CB}}^{2}$
=-$\frac{1}{2}$×12+$\frac{1}{2}$×1×2×cos120°+$\frac{1}{4}$×2×1×cos60°+$\frac{1}{4}$×22
=$\frac{1}{4}$;
②假设存在非零实数λ,使得$\overrightarrow{AE}$⊥$\overrightarrow{CD}$,
由$\overrightarrow{AD}$=λ$\overrightarrow{AB}$,得$\overrightarrow{AD}$=λ($\overrightarrow{CB}$-$\overrightarrow{CA}$),
∴$\overrightarrow{CD}$=$\overrightarrow{CA}$+$\overrightarrow{AD}$=$\overrightarrow{CA}$+λ($\overrightarrow{CB}$-$\overrightarrow{CA}$)=λ$\overrightarrow{CB}$+(1-λ)$\overrightarrow{CA}$;
又$\overrightarrow{BE}$=λ$\overrightarrow{BC}$,
∴$\overrightarrow{AE}$=$\overrightarrow{AB}$+$\overrightarrow{BE}$=($\overrightarrow{CB}$-$\overrightarrow{CA}$)+λ(-$\overrightarrow{CB}$)=(1-λ)$\overrightarrow{CB}$-$\overrightarrow{CA}$;
∴$\overrightarrow{AE}$•$\overrightarrow{CD}$=λ(1-λ)${\overrightarrow{CB}}^{2}$-λ$\overrightarrow{CB}$•$\overrightarrow{CA}$+(1-λ)2$\overrightarrow{CB}$•$\overrightarrow{CA}$-(1-λ)${\overrightarrow{CA}}^{2}$
=4λ(1-λ)-λ+(1-λ)2-(1-λ)
=-3λ2+2λ=0,
解得λ=$\frac{3}{2}$或λ=0(不合题意,舍去);
即存在非零实数λ=$\frac{3}{2}$,使得$\overrightarrow{AE}$⊥$\overrightarrow{CD}$.
点评 本题考查了平面向量的线性表示与数量积的应用问题,也考查了余弦定理的应用问题,是综合性题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
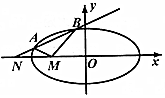 已知椭圆C:$\frac{{x}^{2}}{2}$$+\frac{{y}^{2}}{n}$=1(0<n<2).
已知椭圆C:$\frac{{x}^{2}}{2}$$+\frac{{y}^{2}}{n}$=1(0<n<2).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3} | B. | {-1,3} | C. | {-1,1,3} | D. | {-1,-1,1,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com