练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列函数中，在其定义域内既是奇函数又是增函数的是（ ）
    A.y=x3+x
    B.y=﹣
    C.y=sinx
    D.

    【答案】A
    【解析】解：根据题意，依次分析选项：

    对于A、对于函数f（x）=x3+x，有f（﹣x）=（﹣x）3+（﹣x）=﹣（x3+x）=﹣f（x），为奇函数，

    又由其导数f′（x）=3x2+1＞0，故函数f（x）为增函数，符合题意，

    对于B、函数y=﹣ = ，为反比例函数，在其定义域上不是增函数，不符合题意；

    对于C、y=sinx为正弦函数，在其定义域上不是增函数，不符合题意；

    对于D、y=（ ）x﹣2x=2﹣x﹣2x，在定义域上为减函数，不符合题意；

    故选：A．

    【考点精析】利用奇偶性与单调性的综合对题目进行判断即可得到答案，需要熟知奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】随着网络的发展，人们可以在网络上购物、玩游戏、聊天、导航等，所以人们对上网流量的需求越来越大．某电信运营商推出一款新的“流量包”套餐．为了调查不同年龄的人是否愿意选择此款“流量包”套餐，随机抽取50个用户，按年龄分组进行访谈，统计结果如表．

    组号

    年龄

    访谈人数

    愿意使用

    1

    [18，28）

    4

    4

    2

    [28，38）

    9

    9

    3

    [38，48）

    16

    15

    4

    [48，58）

    15

    12

    5

    [58，68）

    6

    2

    （Ⅰ）若在第2、3、4组愿意选择此款“流量包”套餐的人中，用分层抽样的方法抽取12人，则各组应分别抽取多少人？
    （Ⅱ）若从第5组的被调查者访谈人中随机选取2人进行追踪调查，求2人中至少有1人愿意选择此款“流量包”套餐的概率．
    （Ⅲ）按以上统计数据填写下面2×2列联表，并判断以48岁为分界点，能否在犯错误不超过1%的前提下认为，是否愿意选择此款“流量包”套餐与人的年龄有关？

    年龄不低于48岁的人数

    年龄低于48岁的人数

    合计

    愿意使用的人数

    不愿意使用的人数

    合计

    参考公式： ，其中：n=a+b+c+d．

    P（k2≥k0）

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    k

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某品牌新款夏装即将上市，为了对夏装进行合理定价，在该地区的三家连锁店各进行了两天试销售，得到如下数据：

    连锁店

    A店

    B店

    C店

    售价x（元）

    80

    86

    82

    88

    84

    90

    销售量y（件）

    88

    78

    85

    75

    82

    66


    （1）以三家连锁店分别的平均售价和平均销量为散点，求出售价与销量的回归直线方程 ；
    （2）在大量投入市场后，销售量与单价仍然服从（1）中的关系，且该夏装成本价为40元/件，为使该款夏装在销售上获得最大利润，该款夏装的单价应定为多少元（保留整数）？ ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校为了普及环保知识，增强学生的环保意识，在全校组织了一次有关环保知识的竞赛．经过初赛、复赛，甲、乙两个代表队（每队3人）进入了决赛，规定每人回答一个问题，答对为本队赢得10分，答错得0分．假设甲队中每人答对的概率均为 ，乙队中3人答对的概率分别为 ， ， ，且各人回答正确与否相互之间没有影响，用ξ表示乙队的总得分． （Ⅰ）求ξ的分布列和数学期望；
    （Ⅱ）求甲、乙两队总得分之和等于30分且甲队获胜的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义在R上的函数y=f（x）对任意的x、y∈R，满足条件：f（x+y）=f（x）+f（y）﹣1，且当x＞0时，f（x）＞1．
    （1）求f（0）的值；
    （2）证明：函数f（x）是R上的单调增函数；
    （3）解关于t的不等式f（2t2﹣t）＜1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某池塘养殖着鲤鱼和鲫鱼,为了估计这两种鱼的数量,养殖者从池塘中捕出这两种鱼各1 000条,给每条鱼做上不影响其存活的标记,然后放回池塘,待完全混合后,再每次从池塘中随机地捕出1 000条鱼,记录下其中有记号的鱼的数目,立即放回池塘中.这样的记录做了10次,并将记录获取的数据制作成如图所示的茎叶图.

    (1)根据茎叶图计算有记号的鲤鱼和鲫鱼数目的平均数,并估计池塘中的鲤鱼和鲫鱼的数量;

    (2)为了估计池塘中鱼的总质量,现按照(1)中的比例对100条鱼进行称重,根据称重鱼的质量介于[0,4.5](单位:千克)之间,将测量结果按如下方式分成九组:第一组[0,0.5),第二组[0.5,1),…,第九组[4,4.5].如图是按上述分组方法得到的频率分布直方图的一部分.

    ①估计池塘中鱼的质量在3千克以上(含3千克)的条数;

    ②若第三组鱼的条数比第二组多7条、第四组鱼的条数比第三组多7条,请将频率分布直方图补充完整;

    ③在②的条件下估计池塘中鱼的质量的众数及池塘中鱼的总质量.

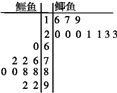
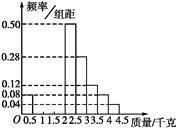
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，菱形ABCD的边长为4，∠BAD=60°，AC∩BD=O，将菱形ABCD沿对角线AC折起，得到三棱锥B﹣ACD，点M是棱BC的中点，且DM=2 ．
    （1）求证：OM∥平面ABD；
    （2）求证：平面DOM⊥平面ABC；
    （3）求点B到平面DOM的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下面是60名男生每分钟脉搏跳动次数的频率分布表.

    分组

    频数

    频率

    [51.5,57.5)

    4

    0.067

    0.011

    [57.5,63.5)

    6

    0.1

    0.017

    [63.5,69.5)

    11

    0.183

    0.031

    [69.5,75.5)

    20

    0.333

    0.056

    [75.5,81.5)

    11

    0.183

    0.031

    [81.5,87.5)

    5

    0.083

    0.014

    [87.5,93.5]

    3

    0.05

    0.008

    (1)作出其频率分布直方图;

    (2)根据直方图的各组中值估计总体平均数;

    (3)估计每分钟脉搏跳动次数的范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在正四面体P﹣ABC体积为V，现内部取一点S，则 的概率为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案