Question

【题目】设椭圆 （ ）的右焦点为F，右顶点为A，已知 ，其中O 为原点， e为椭圆的离心率.
（Ⅰ）求椭圆的方程；
（Ⅱ）设过点A的直线l与椭圆交于点B（B不在x轴上），垂直于l的直线与l交于点M，与y轴交于点H，若 ，且 ，求直线的l斜率.

Answer 1

【答案】解：（I）设 ，由 ，即 ，可得 ，又 ，所以 ，因此 ，所以椭圆的方程为 .
（Ⅱ）设直线的斜率为 ，则直线l的方程为 ，设 ，由方程组 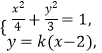消去y，整理得 ，
解得x=2或 ，
由题意得 ，从而 ，
由（1）知 ，设 ，有 ， ，
由 ，得 ，所以 ，
解得 ，因此直线MH的方程为 ，
设 ，由方程组 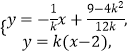消去y，得 ，
在 中， ，
即 ，化简得 ，即 ，
解得 或 ，
所以直线l的斜率为 或
【解析】本题主要考查椭圆的标准方程以及直线与椭圆的位置关系的应用。（1）根据题意画出图形，根据已知的等式找到a，b,c的关系式即可求出椭圆的方程。（2）由已知条件先设出直线的方程，然后联立直线和椭圆的方程，化为关于x的一元二次方程，利用韦达定理求出B点的坐标，再求出H的坐标，然后根据垂直得到向量的数量积为0，进而求出直线方程，再根据角相等可得到线段相等，即可求出斜率的值。
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识，掌握椭圆标准方程焦点在x轴：，焦点在y轴：．