
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,且点
,且点![]() 是该函数图象的一个最高点.
是该函数图象的一个最高点.
(1)求函数![]() 的解析式;
的解析式;
(2)若![]() ,求函数
,求函数![]() 的值域;
的值域;
(3)把函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 在
在![]() 上是单调增函数,求
上是单调增函数,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)由![]() 是该函数图象的一个最高点求出
是该函数图象的一个最高点求出![]() ,由周期为
,由周期为![]() 求出
求出![]() ,由特殊点的坐标求出
,由特殊点的坐标求出![]() 的值,从而可得函数的解析式;(2)由
的值,从而可得函数的解析式;(2)由![]() 可求的
可求的![]() ,利用正弦函数的性质可求其值域;(3)利用三角函数平移变换规律可求
,利用正弦函数的性质可求其值域;(3)利用三角函数平移变换规律可求![]() ,利用正弦函数的单调性可求函数的单调递增区间,进而可得
,利用正弦函数的单调性可求函数的单调递增区间,进而可得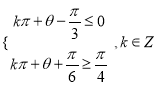 ,结合范围
,结合范围![]() ,可求
,可求![]() 的取值范围.
的取值范围.
试题解析:(1)∵由题意可得,A=2,![]() =π,∴ω=2.
=π,∴ω=2.
∵再根据函数的图象经过点M(![]() ,2),可得2sin(2×
,2),可得2sin(2×![]() +φ)=2,结合|φ|<
+φ)=2,结合|φ|<![]() ,可得
,可得![]() =
=![]() ,∴f(x)=2sin(2x+
,∴f(x)=2sin(2x+![]() ).
).
(2)∵x∈[﹣![]() ,0],
,0],
∴2x+![]() ∈[﹣
∈[﹣![]() ,
,![]() ],
],
∴sin(2x+![]() )∈[﹣1,
)∈[﹣1,![]() ],可得:f(x)=2sin(2x+
],可得:f(x)=2sin(2x+![]() )∈[﹣2,1].(3)把函数y=f(x)的图线向右平移θ(0<θ<
)∈[﹣2,1].(3)把函数y=f(x)的图线向右平移θ(0<θ<![]() )个单位,
)个单位,
得到函数y=g(x)=2sin[2(x﹣θ)+![]() ]=2sin(2x﹣2θ+
]=2sin(2x﹣2θ+![]() ),
),
∴令2kπ﹣![]() ≤2x﹣2θ+
≤2x﹣2θ+![]() ≤2kπ+
≤2kπ+![]() ,k∈Z,解得:kπ+θ﹣
,k∈Z,解得:kπ+θ﹣![]() ≤x≤kπ+θ+
≤x≤kπ+θ+![]() ,k∈Z,
,k∈Z,
可得函数的单调递增区间为:[kπ+θ﹣![]() ,kπ+θ+
,kπ+θ+![]() ],k∈Z,
],k∈Z,
∵函数y=g(x)在[0,![]() ]上是单调增函数,∴
]上是单调增函数,∴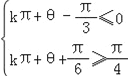 ,
,
∴解得: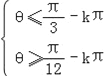 ,k∈Z,∵0<θ<
,k∈Z,∵0<θ<![]() ,
,![]() ,∴当k=0时,θ∈[
,∴当k=0时,θ∈[![]() ,].
,].


科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>0)的焦点在x轴上,且椭圆C的焦距为2. (Ⅰ)求椭圆C的标准方程;
=1(a>0)的焦点在x轴上,且椭圆C的焦距为2. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)过点R(4,0)的直线l与椭圆C交于两点P,Q,过P作PN⊥x轴且与椭圆C交于另一点N,F为椭圆C的右焦点,求证:三点N,F,Q在同一条直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣3x2 . (Ⅰ) 求f(x)的单调区间;
(Ⅱ) 若f(x)的定义域为[﹣1,m]时,值域为[﹣4,0],求m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB=BC,D为线段AC的中点.

(1)求证:PA⊥BD.
(2)求证:BD⊥平面PAC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com