
【题目】已知函数 ![]() 在区间[﹣
在区间[﹣ ![]() ,
, ![]() ]上有f(x)>0恒成立,则a的取值范围为( )
]上有f(x)>0恒成立,则a的取值范围为( )
A.(0,2]
B.[2,+∞)
C.(0,5)
D.(2,5]
【答案】C
【解析】解:∵函数f(x)=ax3﹣ ![]() x2+1,(x∈R,a>0)
x2+1,(x∈R,a>0)
∴f′(x)=3ax2﹣3x,
由f′(x)=0,得x=0,或x= ![]() ,
,
①当 ![]() ≥
≥ ![]() ,0<a≤2时,
,0<a≤2时,
∵f(﹣ ![]() )=
)= ![]() ﹣
﹣ ![]() ,f(
,f( ![]() )=
)= ![]() +
+ ![]() ,f(0)=1,
,f(0)=1,
∴在区间[﹣ ![]() ,
, ![]() ]上,f(x)min=
]上,f(x)min= ![]() ﹣
﹣ ![]() ,
,
∵在区间[﹣ ![]() ,
, ![]() ]上,f(x)>0恒成立,
]上,f(x)>0恒成立,
∴f(x)min= ![]() ﹣
﹣ ![]() >0,解得a<5,
>0,解得a<5,
∴0<a≤2.
②当 ![]() <
< ![]() ,a>2时,
,a>2时,
∵f(﹣ ![]() )=
)= ![]() ﹣
﹣ ![]() ,f(
,f( ![]() )=
)= ![]() +
+ ![]() ,f(0)=1,f(
,f(0)=1,f( ![]() )=1﹣
)=1﹣ ![]() ,
,
∴在区间[﹣ ![]() ,
, ![]() ]上,f(x)min=
]上,f(x)min= ![]() ﹣
﹣ ![]() ,
,
∵在区间[﹣ ![]() ,
, ![]() ]上,f(x)>0恒成立,
]上,f(x)>0恒成立,
∴f(x)min= ![]() ﹣
﹣ ![]() >0,解得a<5,
>0,解得a<5,
∴2<a<5.
综上所述,a的取值范围是(0,5),
故选:C.
【考点精析】本题主要考查了函数的最大(小)值与导数的相关知识点,需要掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
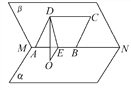
【题目】如图,已知二面角α-MN-β的大小为60°,菱形ABCD在平面β内,A,B两点在棱MN上,∠BAD=60°,E是AB的中点,DO⊥平面α,垂足为O.
(1)证明:AB⊥平面ODE.
(2)求异面直线BC与OD所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)判断函数![]() 的奇偶性,并给出证明;
的奇偶性,并给出证明;
(2)解不等式: ![]() ;
;
(3)若函数![]() 在
在![]() 上单调递减,比较f(2)+f(4)+…+f(2n)与2n(n∈N*)的大小关系,并说明理由.
上单调递减,比较f(2)+f(4)+…+f(2n)与2n(n∈N*)的大小关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足: ![]() ,anan+1<0(n≥1),数列{bn}满足:bn=an+12﹣an2(n≥1). (Ⅰ)求数列{an},{bn}的通项公式
,anan+1<0(n≥1),数列{bn}满足:bn=an+12﹣an2(n≥1). (Ⅰ)求数列{an},{bn}的通项公式
(Ⅱ)证明:数列{bn}中的任意三项不可能成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大衍数列,来源于中国古代著作《乾坤谱》中对易传“大衍之数五十”的推论.其前10项为:0、2、4、8、12、18、24、32、40、50.通项公式: 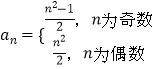 ,如果把这个数列{an}排成如图形状,并记A(m,n)表示第m行中从左向右第n个数,则A(10,4)的值为( )
,如果把这个数列{an}排成如图形状,并记A(m,n)表示第m行中从左向右第n个数,则A(10,4)的值为( ) 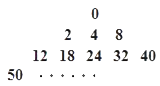
A.1200
B.1280
C.3528
D.3612
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,且点
,且点![]() 是该函数图象的一个最高点.
是该函数图象的一个最高点.
(1)求函数![]() 的解析式;
的解析式;
(2)若![]() ,求函数
,求函数![]() 的值域;
的值域;
(3)把函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 在
在![]() 上是单调增函数,求
上是单调增函数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=lnx,g(x)=f(x)+f′(x). (Ⅰ)求g(x)的单调区间和最小值;
(Ⅱ)讨论g(x)与 ![]() 的大小关系;
的大小关系;
(Ⅲ)求a的取值范围,使得g(a)﹣g(x)< ![]() 对任意x>0成立.
对任意x>0成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
设某旅游景点每天的固定成本为500元,门票每张为30元,变动成本与购票进入旅游景点的人数的算术平方根成正比。一天购票人数为25时,该旅游景点收支平衡;一天购票人数超过100时,该旅游景点须另交保险费200元。设每天的购票人数为![]() ,盈利额为
,盈利额为![]() 元。
元。
(Ⅰ)求![]() 与
与![]() 之间的函数关系;
之间的函数关系;
(Ⅱ)该旅游景点希望在人数达到20人时即不出现亏损,若用提高门票价格的措施,则每张门票至少要多少元(取整数)?
(参考数据:![]() .)
.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com