已知函数f(x)=ex-ln(x+1)-1(x≥0),
(1)求函数f(x)的最小值;
(2)若0≤y<x,求证:ex-y-1>ln(x+1)-ln(y+1)
解:(1)f′(x)=
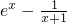
,…(2分)
当x≥0时,
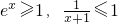
,所以当x≥0时,f′(x)≥0,
则函数f(x)在[0,+∞)上单调递增,
所以函数f(x)的最小值f(0)=0;…(5分)
(2)由(1)知,当x>0时,f(x)>0,
∵x>y,
∴f(x-y)=e
x-y-ln(x-y+1)-1>0,e
x-y-1>ln(x-y+1)①…(7分)
∵
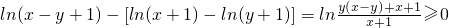
,
∴ln(x-y+1)≥ln(x+1)-ln(y+1)②…(10分)
由①②得 e
x-y-1>ln(x+1)-ln(y+1)…(12分)
分析:(1)先求导函数,确定函数在定义域内的单调性,从而可求函数f(x)的最小值;
(2)利用(1)的结论,当x>0时,f(x)>0,可得f(x-y)=e
x-y-ln(x-y+1)-1>0,从而e
x-y-1>ln(x-y+1)再证明ln(x-y+1)≥ln(x+1)-ln(y+1)即可.
点评:本题以函数为载体,考查函数的最值,考查导数的运用,考查不等式的证明,有一定的综合性.

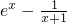 ,…(2分)
,…(2分)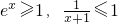 ,所以当x≥0时,f′(x)≥0,
,所以当x≥0时,f′(x)≥0,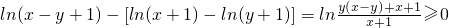 ,
,
