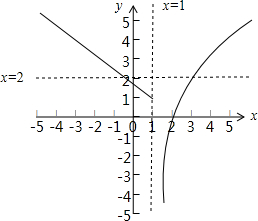Question

已知函数f（x）=

k(x-1)+1，x≤1 ln(x-1)，x＞1

，则当k＜0时函数y=f（f（x））有

 

个零点．

Answer 1

考点：根的存在性及根的个数判断

专题：函数的性质及应用

分析：根据已知中函数的解析式，分析函数的图象及性质，画出函数的草图，进而将函数y=f（f（x））零点的个数转化f（x）=2解的个数，数形结合可得答案．

解答： 解：∵k＜0，
故当x≤1时，f（x）=k（x-1）+1≥f（1）=1，
即此时f（x）无零点，
当x＞1时，f（2）=ln（2-1）=ln1=0，
即此时f（x）有一个零点，
故函数f（x）=

k(x-1)+1，x≤1 ln(x-1)，x＞1

的草图如下所示：
综上函数y=f（f（x））零点的个数，即f（x）=2解的个数，

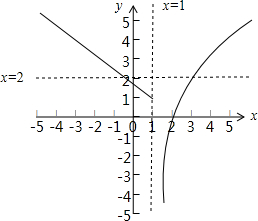
由图可得，f（x）=2有两个解，
故函数y=f（f（x））有两个零点，
故答案为：2．

点评：本题考查的知识点是函数的图象和性质，函数零点，其中将函数y=f（f（x））零点的个数转化f（x）=2解的个数，是解答的关键．