
如图,在圆 上任取一点
上任取一点 ,过点
,过点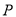 作
作 轴的垂线段
轴的垂线段 ,
, 为垂足.设
为垂足.设 为线段
为线段 的中点.
的中点.
(1)当点 在圆
在圆 上运动时,求点
上运动时,求点 的轨迹
的轨迹 的方程;
的方程;
(2)若圆 在点
在点 处的切线与
处的切线与 轴交于点
轴交于点 ,试判断直线
,试判断直线 与轨迹
与轨迹 的位置关系.
的位置关系.

(1) ;(2)相切
;(2)相切
【解析】
试题分析:(1)由于点 在圆
在圆 上运动,
上运动,  为线段
为线段 的中点,根据两点坐标的关系,以及点P在圆上,即可得到结论.
的中点,根据两点坐标的关系,以及点P在圆上,即可得到结论.
(2)由(1)得到轨迹 的方程为椭圆方程.切线PE的斜率有两种情况:斜率不存在则可得直线
的方程为椭圆方程.切线PE的斜率有两种情况:斜率不存在则可得直线 与轨迹
与轨迹 的位置关系为相切.直线斜率存在则假设点P的坐标,写出切线方程,以及点N的坐标,再写出直线MN的方程.联立椭圆方程,根据判别式的值即可得到结论.
的位置关系为相切.直线斜率存在则假设点P的坐标,写出切线方程,以及点N的坐标,再写出直线MN的方程.联立椭圆方程,根据判别式的值即可得到结论.
(1)设 ,则
,则 .
. 点
点 在圆
在圆 上,
上, ,
,
即点 的轨迹
的轨迹 的方程为
的方程为 . 4分
. 4分
(2)解法一:
(i) 当直线 的斜率不存在时,直线
的斜率不存在时,直线 的方程为
的方程为 或
或 .显然与轨迹
.显然与轨迹 相切;
相切;
(2)当直线 的斜率存在时,设
的斜率存在时,设 的方程为
的方程为 ,
,
因为直线 与圆
与圆 相切,所以
相切,所以 ,即
,即 . 7分
. 7分
又直线 的斜率等于
的斜率等于 ,点
,点 的坐标为
的坐标为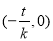 .
.
所以直线 的方程为
的方程为 ,即
,即 . 9分
. 9分
由 得
得 .
.

 .故直线
.故直线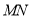 与轨迹
与轨迹 相切.
相切.
综上(i)(2)知,直线 与轨迹
与轨迹 相切. 13分
相切. 13分
解法二 :设 (
( ),则
),则 . 5分
. 5分
(i)当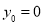 时,直线
时,直线 的方程为
的方程为 或
或 ,此时,直线
,此时,直线 与轨迹
与轨迹 相切;
相切;
(2)当 时,直线
时,直线 的方程为
的方程为 ,即
,即 .
.
令 ,则
,则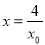 .
. ,又点
,又点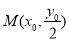 ,
,
所以直线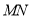 的方程为
的方程为 ,即
,即 . 9分
. 9分
由 得
得 即
即 .
.
 .所以,直线
.所以,直线 与轨迹
与轨迹 相切.
相切.
综上(i)(2)知,直线 与轨迹
与轨迹 相切. 13分
相切. 13分
考点:1.待定系数法求椭圆的方程.2.直线与圆的位置关系.3.直线与椭圆的位置关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2013-2014学年福建省龙岩市高三上学期期末考试文科数学试卷(解析版) 题型:解答题
如图所示,在直径为BC的半圆中,A是弧BC上一点,正方形PQRS内接于△ABC,若BC=a,∠ABC=θ,设△ABC的面积为Sl,正方形PQRS的面积为S2.

(1)用a,θ表示S1和S2;
(2)当a固定,θ变化时,求 取得最小值时θ的值.
取得最小值时θ的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省龙岩市高三上学期期末考试文科数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,若输入m的值为8,则输出s的值为( )

A. 4 B. 6 C. 8 D. 16
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高三高考压轴理科数学试卷(解析版) 题型:填空题
小明在做一道数学题目时发现:若复数
 ,
, (其中
(其中 ), 则
), 则 ,
, ,根据上面的结论,可以提出猜想: z1·z2·z3= .
,根据上面的结论,可以提出猜想: z1·z2·z3= .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高三高考压轴理科数学试卷(解析版) 题型:选择题
如图,在△ABC中,AB=3,AC=5,若O为△ABC的外心,则 的值是(( )
的值是(( )

A.4 B. 8 C.6
B. 8 C.6 D.6
D.6
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高三高考压轴文科数学试卷(解析版) 题型:选择题
若变量 满足约束条件
满足约束条件 且
且 的最大值为
的最大值为 ,最小值为b,则
,最小值为b,则 的值是( )
的值是( )
A.10 B.20 C.4 D.12

查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省福州市高三5月综合练习文科数学试卷(解析版) 题型:选择题
已知 都是定义在R上的函数,
都是定义在R上的函数,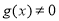 ,
, ,且
,且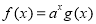 (
( ),
),  ,对于数列
,对于数列 (n=1,2, ,10),任取正整数k(1≤k≤10),则其前k项和大于
(n=1,2, ,10),任取正整数k(1≤k≤10),则其前k项和大于 的概率是( ).
的概率是( ).
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com