
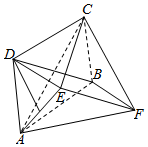
 如图,将菱形AECF沿对角线EF折叠,分别过E、F作AC所在平面的垂线ED、FB,垂足分别为D、B,四边形ABCD为菱形,且∠BAD=60°.
如图,将菱形AECF沿对角线EF折叠,分别过E、F作AC所在平面的垂线ED、FB,垂足分别为D、B,四边形ABCD为菱形,且∠BAD=60°.分析 (1)可通过证明平面BCF∥平面ADE来得出FC∥平面ADE;
(2)利用勾股定理证明DE=BF,得出四边形BDEF是矩形再证明AC⊥平面BDEF,于是几何体分割成全等的两个四棱锥A-BDEF和C-BDEF.
解答 证明:(1)∵DE⊥平面ABCD,BF⊥平面ABCD,
∴DE∥BF,又BF?平面ADE,DE?平面ADE,
∴BF∥平面ADE.
∵四边形ABCD是菱形,∴BC∥AD,
又BC?平面ADE,AD?平面ADE,
∴BC∥平面ADE,
又BF?平面BCF,BC?平面BCF,BC∩BF=B,
∴平面BCF∥平面ADE,∵CF?平面BCF,
∴FC∥平面ADE.
(2)∵四边形ABCD是菱形,∠BAD=60°,AB=2,
∴△ABD是等边三角形,AC⊥BD,
∴AC=2$\sqrt{3}$,BD=AD=BC=2,
∵DE⊥平面ABCD,BF⊥平面ABCD,
∴DE⊥AD,BF⊥BC,DE⊥BD,DE⊥AC,
∴AC⊥平面BDEF,DE=$\sqrt{A{E}^{2}-A{D}^{2}}$,BF=$\sqrt{C{F}^{2}-B{C}^{2}}$,
又折叠前AECF是菱形,∴AE=CF,
∴DE=BF,又DE∥CF,∴四边形BDEF是矩形.
∴S矩形BDEF=BD•BF=2×1=2.
∴几何体的体积V=$\frac{1}{3}{S}_{矩形BDEF}$•AC=$\frac{1}{3}×2×2\sqrt{3}$=$\frac{4\sqrt{3}}{3}$.
点评 本题考查了线面平行的判定,棱锥的体积计算,当不好构造平行直线时,常采用证明面面平行得出线面平行,属于中档题.


科目:高中数学 来源: 题型:解答题
| 运动时间 性别 | 运动达人 | 非运动达人 | 合计 |
| 男生 | 36 | ||
| 女生 | 26 | ||
| 合计 | 100 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 144 | B. | 288 | C. | 480 | D. | 720 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{3}+1}{2}$ | D. | $\sqrt{3}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某商店有标号为0到9的10个气球
某商店有标号为0到9的10个气球查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com