
 某商店有标号为0到9的10个气球
某商店有标号为0到9的10个气球分析 (Ⅰ)分两类,第一类,当末尾是0时,当末尾是5时,根据分类计数原理可得.
(Ⅱ)分情况讨论,根据分类计数原理可得,
(Ⅲ)一种射击方案对应于从0至9共十个数字中取2个、3个、3个、2个数字的组合,因为每组数的数字大小是固定的,数字小的挂下面,可得结论
解答 (Ⅰ)第一类,当末尾是0时,其它3个位置任意排,故有A93=504种,
当末尾是5时,首位有8种选择,其它2个位置任意排,故有8A82=448种,
根据分类计数原理,共有504+448=952种;
(Ⅱ)01连在一起时有15中情况;12连在一起时有10种情况;23连在一起有11种情况;34连在一起有11种情况;45连在一起有11种情况;
56和34一样,67和23一样;78和12一样;89和01一样,共有105种
(Ⅲ)一种射击方案对应于从0至9共十个数字中取2个、3个、3个、2个数字的组合,因为每组数的数字大小是固定的,数字小的挂下面.
所以共有C102C82C53=25200
点评 本题考查排列、组合的实际应用,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
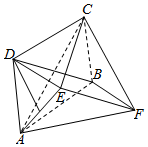 如图,将菱形AECF沿对角线EF折叠,分别过E、F作AC所在平面的垂线ED、FB,垂足分别为D、B,四边形ABCD为菱形,且∠BAD=60°.
如图,将菱形AECF沿对角线EF折叠,分别过E、F作AC所在平面的垂线ED、FB,垂足分别为D、B,四边形ABCD为菱形,且∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
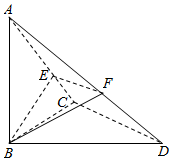 如图,已知ABCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别AC,AD是上的动点,且$\frac{AE}{AC}$=$\frac{AF}{AD}$=λ(0<λ<1).
如图,已知ABCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别AC,AD是上的动点,且$\frac{AE}{AC}$=$\frac{AF}{AD}$=λ(0<λ<1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若f(a)≤|b|,则a≤b | B. | 若f(a)≤2b,则a≤b | C. | 若f(a)≥|b|,则a≥b | D. | 若f(a)≥2b,则a≥b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com