Question

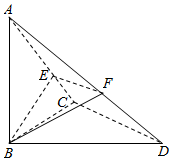
16．如图，已知ABCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E，F分别AC，AD是上的动点，且$\frac{AE}{AC}$=$\frac{AF}{AD}$=λ（0＜λ＜1）．
（Ⅰ）求证：不论λ为何值，总有EF⊥平面ABC；
（Ⅱ）若三棱锥A-BEF的体积为$\frac{{\sqrt{6}}}{12}$，求此时λ的值．

Answer 1

分析 （1）要证不论λ为何值，总有EF⊥平面ABC，只需证CD⊥平面ABC，在△BCD中，根据∠BCD=90°得证．
（2）根据$V=\frac{1}{3}{S_{△AEB}}•EF=\frac{1}{3}•\frac{{\sqrt{6}}}{2}•{λ^2}=\frac{{\sqrt{6}}}{12}$，即可求此时λ的值．

解答 （I）证明：因为AB⊥平面BCD，所以AB⊥CD，
又在△BCD中，∠BCD=90°，所以，BC⊥CD，又AB∩BC=B，
所以，CD⊥平面ABC，
又在△ACD，E、F分别是AC、AD上的动点，且$\frac{AE}{AC}$=$\frac{AF}{AD}$=λ（0＜λ＜1）
所以，不论λ为何值，总有EF⊥平面ABC…（6分）
（II）解：$|BD|=\sqrt{|BC{|^2}+|CD{|^2}}=\sqrt{2}$，$|AB|=\sqrt{3}|BD|=\sqrt{6}$，${S_{△ABC}}=\frac{{\sqrt{6}}}{2}$．
${S_{△AEB}}=λ•{S_{△ABC}}=\frac{{\sqrt{6}}}{2}λ$，h=|EF|=λ•|CD|=λ，
所以$V=\frac{1}{3}{S_{△AEB}}•EF=\frac{1}{3}•\frac{{\sqrt{6}}}{2}•{λ^2}=\frac{{\sqrt{6}}}{12}$
解之得$λ=\frac{{\sqrt{2}}}{2}$…（12分）

点评 本题考查考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力．属于中档题．