
| X1 | 6 | 7 | 8 | 9 | 10 |
| P | 0.16 | 0.14 | 0.42 | 0.1 | 0.18 |
| X2 | 6 | 7 | 8 | 9 | 10 |
| P | 0.19 | 0.24 | 0.12 | 0.28 | 0.17 |
分析 由离散型随机变量的分布列的性质,先分别求出E(X1)、E(X2)、D(X1)、D(X2),从而得到甲、乙两名射手的平均成绩相等,但甲选手比乙选手成绩更稳定.
解答 解:由题意,得:
E(X1)=6×0.16+7×0.14+8×0.42+9×0.1+10×0.18=8,
D(X1)=(6-8)2×0.16+(7-8)2×0.14+(8-8)2×0.42+(9-8)2×0.1+(10-8)2×0.18=1.6.
E(X2)=6×0.19+7×0.24+8×0.12+9×0.28+10×0.17=8,
D(X2)=(6-8)2×0.19+(7-8)2×0.24+(8-8)2×0.12+(9-8)2×0.28+(10-8)2×0.17=1.96.
∵E(X1)=E(X2),D(X1)<D(X2),
∴甲、乙两名射手的平均成绩相等,但甲选手比乙选手成绩更稳定.
点评 本题考查离散型随机变量的均值和方差的求法及应用,是基础题,解题时要认真审题,注意离散型随机变量的分布列的性质的合理运用.


科目:高中数学 来源: 题型:解答题
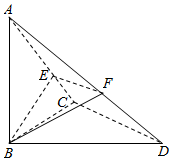 如图,已知ABCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别AC,AD是上的动点,且$\frac{AE}{AC}$=$\frac{AF}{AD}$=λ(0<λ<1).
如图,已知ABCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别AC,AD是上的动点,且$\frac{AE}{AC}$=$\frac{AF}{AD}$=λ(0<λ<1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若f(a)≤|b|,则a≤b | B. | 若f(a)≤2b,则a≤b | C. | 若f(a)≥|b|,则a≥b | D. | 若f(a)≥2b,则a≥b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,在△ABC中,D为边AC的中点,BC=3BE,其中AE与BD交于O点,延长CO交边AB于F点,则$\frac{FO}{OC}$=$\frac{1}{3}$.
如图所示,在△ABC中,D为边AC的中点,BC=3BE,其中AE与BD交于O点,延长CO交边AB于F点,则$\frac{FO}{OC}$=$\frac{1}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
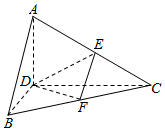 正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,长方体ABCD-A1B1C1D1中,AB=AD=1.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com