
 如图,长方体ABCD-A1B1C1D1中,AB=AD=1.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1.分析 (1)确定∠ABD为异面直线A1B1与BD所成角,即可得出结论;
(2)在Rt△B1BA中,AB=1,∠B1AB=60°,求出B1B,利用V=$\frac{1}{3}{S}_{△ABC}•B{B}_{1}$求出三棱锥B1-ABC的体积.
解答 解:(1)∵A1B1∥AB,
∴∠ABD为异面直线A1B1与BD所成角,
∵ABCD为矩形,AB=AD,
∴∠ABD=45°,
∴异面直线A1B1与BD所成角为45°;
(2)在Rt△B1BA中,AB=1,∠B1AB=60°,
∴B1B=$\sqrt{3}$,
∴三棱锥B1-ABC的体积V=$\frac{1}{3}{S}_{△ABC}•B{B}_{1}$=$\frac{1}{3}×\frac{1}{2}×1×1×\sqrt{3}$=$\frac{\sqrt{3}}{6}$.
点评 本题在长方体中求异面直线所成角,并求四面体的体积,着重考查了长方体的性质、异面直线所成角和体积的求法等知识,属于基础题.


科目:高中数学 来源: 题型:解答题
| X1 | 6 | 7 | 8 | 9 | 10 |
| P | 0.16 | 0.14 | 0.42 | 0.1 | 0.18 |
| X2 | 6 | 7 | 8 | 9 | 10 |
| P | 0.19 | 0.24 | 0.12 | 0.28 | 0.17 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
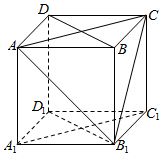 如图,在棱长为1的正方体ABCD-A1B1C1D1中.
如图,在棱长为1的正方体ABCD-A1B1C1D1中.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
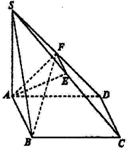 如图,四边形ABCD为矩形,SA⊥平面ABCD,E、F分别是SC、SD的中点,$SA=AD=2,AB=\sqrt{6}$,
如图,四边形ABCD为矩形,SA⊥平面ABCD,E、F分别是SC、SD的中点,$SA=AD=2,AB=\sqrt{6}$,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
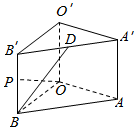 如图所示,在直三棱柱ABO-A′B′O′中,OO′=4,OA=4,OB=3,∠AOB=90°,D是线段A′B′的中点,P是侧棱BB′上的一点,若OP⊥BD,求OP与底面AOB所成角的正切值.
如图所示,在直三棱柱ABO-A′B′O′中,OO′=4,OA=4,OB=3,∠AOB=90°,D是线段A′B′的中点,P是侧棱BB′上的一点,若OP⊥BD,求OP与底面AOB所成角的正切值.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:(单位:万元)
为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:(单位:万元)| 收入x | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
| 支出y | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com