
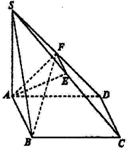
 如图,四边形ABCD为矩形,SA⊥平面ABCD,E、F分别是SC、SD的中点,$SA=AD=2,AB=\sqrt{6}$,
如图,四边形ABCD为矩形,SA⊥平面ABCD,E、F分别是SC、SD的中点,$SA=AD=2,AB=\sqrt{6}$,分析 (1)由SA⊥平面ABCD可得SA⊥CD,又CD⊥AD,从而得出CD⊥平面SAD,于是CD⊥SD,由中位线定理得CD∥EF,故EF⊥SD,由三角形三线合一得AF⊥SD,故而SD⊥平面AEF;
(2)VF-AED=VE-ADF=$\frac{1}{3}{S}_{△ADF}•\frac{1}{2}CD$.
解答 证明:(1)∵SA=AD,F为SD的中点,
∴SD⊥AF,
∵E,F是SC,SD的中点,
∴EF∥CD,
∵SA⊥平面ABCD,CD?平面ABCD,
∴CD⊥SA.
又∵CD⊥AD,SA?平面SAD,AD?平面SAD,SA∩AD=A,
∴CD⊥平面SAD,∵SD?平面SAD,
∴CD⊥SD,
∴EF⊥SD,
∵AF?平面AEF,EF?平面AEF,AF∩EF=F,
∴SD⊥平面AEF.
(2)∵F是SD的中点,
∴SADF=$\frac{1}{2}{S}_{△SAD}$=$\frac{1}{2}×\frac{1}{2}×2×2$=1,
∵E为SC的中点,
∴E到平面SAD的距离h=$\frac{1}{2}CD=\frac{\sqrt{6}}{2}$,
∴VF-AED=VE-ADF=$\frac{1}{3}{S}_{△ADF}•\frac{1}{2}CD$=$\frac{1}{3}×1×\frac{\sqrt{6}}{2}=\frac{\sqrt{6}}{6}$.
点评 本题考查了线面垂直的判定,棱锥的体积计算,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
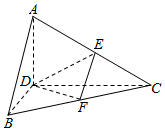 正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知三棱柱ABC-A′B′C′中,平面BCC′B′⊥底面ABC,BB′⊥AC,底面ABC是边长为2的等边三角形,AA′=3,E、F分别在棱AA′,CC′上,且AE=C′F=2.
已知三棱柱ABC-A′B′C′中,平面BCC′B′⊥底面ABC,BB′⊥AC,底面ABC是边长为2的等边三角形,AA′=3,E、F分别在棱AA′,CC′上,且AE=C′F=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,长方体ABCD-A1B1C1D1中,AB=AD=1.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
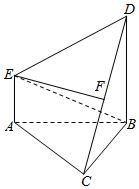 如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,CD与平面ABDE所成角的正弦值为$\frac{{\sqrt{6}}}{4}$.
如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,CD与平面ABDE所成角的正弦值为$\frac{{\sqrt{6}}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
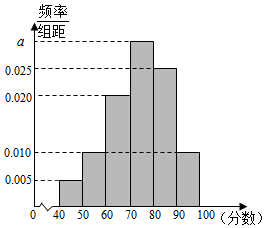 某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100]后得到如图的频率分布直方图.
某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100]后得到如图的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com