
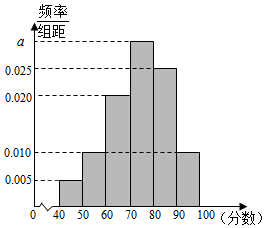
 某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100]后得到如图的频率分布直方图.
某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100]后得到如图的频率分布直方图.分析 (1)根据阴影矩形的面积之和等于1,计算a的值;
(2)首先计算成绩不低于60分的频率,即后四个小矩形的面积和,然后用640×频率计算人数;
(3)若两名学生的学生成绩之差的绝对值不大于10,即两人是同一组的学生,那么首先计算两组的人数,并编号,并以编号的形式列出所有选取2人的基本事件的个数,同时计算同一组的两个人的所有基本事件的个数,最后相除得到概率.
解答 (1)解:由于图中所有小矩形的面积之和等于1,
∴10×(0.005+0.01+0.02+a+0.025+0.01)=1.
解得a=0.03.
(2)解:根据频率分布直方图,成绩不低于6(0分)的频率为
1-10×(0.005+0.01)=0.85.
由于该校高一年级共有学生640人,利用样本估计总体的思想,
可估计该校高一年级数学成绩不低于6(0分)的人数约为640×0.85=544人.
(3)解:成绩在[40,50)分数段内的人数为40×0.05=2人,分别记为A,B.
成绩在[90,100]分数段内的人数为40×0.1=4人,分别记为C,D,E,F.(7分)
若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,
则所有的基本事件有:(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),
(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共15种.(9分)
如果两名学生的数学成绩都在[40,50)分数段内或都在[90,100]分数段内,
那么这两名学生的数学成绩之差的绝对值一定不大于10.
如果一个成绩在[40,50)分数段内,另一个成绩在[90,100]分数段内,
那么这两名学生的数学成绩之差的绝对值一定大于10.
记“这两名学生的数学成绩之差的绝对值不大于10”为事件M,
则事件M包含的基本事件有:
(A,B),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共7种.
所以所求概率为P(M)=$\frac{7}{15}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,是中档题,解题时要认真审题,注意列举法的合理运用.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:解答题
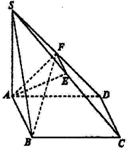 如图,四边形ABCD为矩形,SA⊥平面ABCD,E、F分别是SC、SD的中点,$SA=AD=2,AB=\sqrt{6}$,
如图,四边形ABCD为矩形,SA⊥平面ABCD,E、F分别是SC、SD的中点,$SA=AD=2,AB=\sqrt{6}$,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
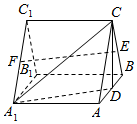 如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等,D,E,F分别为棱AB,BC,A1C1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等,D,E,F分别为棱AB,BC,A1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,-$\frac{1}{2}$] | B. | [-1,0] | C. | [0,1] | D. | [1,$\frac{3}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 气温x(℃) | 18 | 13 | 10 | -1 |
| 用电量y(度) | 24 | 34 | 38 | 64 |
| A. | 68 | B. | 67 | C. | 66 | D. | 65 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com