
分析 (1)设g(x)=ax2+bx+c,根据导数与函数的极值的关系列方程组解出a,b,c;
(2)求出f(x)的解析式,利用导数判断f(x)在[-3,1]上的单调性,求出f(x)的极值和端点函数值,得出最值.
解答 解:(1)设g(x)=ax2+bx+c,则g′(x)=2ax+b,
∵g′(x)的图象与y=2x平行,
∴a=1,
∵y=g(x)在x=-1处取得极小值-5,
∴g′(-1)=-2+b=0,解得b=2.
g(-1)=1-2+c=-5,解得c=-4.
∴g(x)=x2+2x-4.
(2)f(x)=x(x2+2x-4)=x3+2x2-4x.
f′(x)=3x2+4x-4,
令f′(x)=0,解得x=$\frac{2}{3}$或x=-2.
当-3≤x<-2时,f′(x)>0,当-2<x<$\frac{2}{3}$时,f′(x)<0,当$\frac{2}{3}$<x≤1时,f′(x)>0.
∴f(x)在[-3,-2]上单调递增,在(-2,$\frac{2}{3}$)上单调递减,在[$\frac{2}{3}$,1]上单调递增.
∴当x=-2时,f(x)取得极大值f(-2)=8,当x=$\frac{2}{3}$时,f(x)取得极小值f($\frac{2}{3}$)=-$\frac{40}{27}$.
又f(-3)=3,f(1)=-1.
∴f(x)在[-3,1]上的最大值为8,最小值为-$\frac{40}{27}$.
点评 本题考查了导数与函数单调性,函数极值的关系,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| X1 | 6 | 7 | 8 | 9 | 10 |
| P | 0.16 | 0.14 | 0.42 | 0.1 | 0.18 |
| X2 | 6 | 7 | 8 | 9 | 10 |
| P | 0.19 | 0.24 | 0.12 | 0.28 | 0.17 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
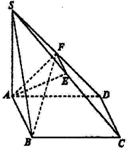 如图,四边形ABCD为矩形,SA⊥平面ABCD,E、F分别是SC、SD的中点,$SA=AD=2,AB=\sqrt{6}$,
如图,四边形ABCD为矩形,SA⊥平面ABCD,E、F分别是SC、SD的中点,$SA=AD=2,AB=\sqrt{6}$,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
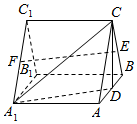 如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等,D,E,F分别为棱AB,BC,A1C1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等,D,E,F分别为棱AB,BC,A1C1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com