
分析 首先利用定积分的运算法则写成各部分定积分的和,然后分别利用定积分的几何意义,函数奇偶性以及求原函数的方法求定积分值.
解答 解:${∫}_{-1}^{1}$($\sqrt{16-(x+3)^{2}}$+$\frac{{e}^{x}-1}{{e}^{x}+1}$-x2)dx=${∫}_{-1}^{1}\sqrt{16-(x+3)^{2}}dx$+${∫}_{-1}^{1}\frac{{e}^{x}-1}{{e}^{x}+1}dx-{∫}_{-1}^{1}{x}^{2}dx$
=($\frac{1}{6}π×{4}^{2}-\frac{1}{2}×2×2\sqrt{3}$)+0-$\frac{1}{3}{x}^{3}{|}_{-1}^{1}$
=$\frac{8}{3}π-2\sqrt{3}-\frac{2}{3}$;
故答案为:$\frac{8}{3}π-2\sqrt{3}-\frac{2}{3}$.
点评 本题考查了定积分的计算;分别利用了定积分的运算法则以及利用几何意义求定积分、函数的奇偶性;关键是正确找出被积函数的原函数.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
 如图,某构件是由编号1、2、…、k(k∈N*且k≥3)的有限个圆柱自下而上组成的,其中每一个圆柱的高与其底面圆的直径相等,且对于任意两个相邻圆柱,上面圆柱的高是下面圆柱的高的一半,设编号1的圆柱的高为4.
如图,某构件是由编号1、2、…、k(k∈N*且k≥3)的有限个圆柱自下而上组成的,其中每一个圆柱的高与其底面圆的直径相等,且对于任意两个相邻圆柱,上面圆柱的高是下面圆柱的高的一半,设编号1的圆柱的高为4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某企业有员工1000名,为了丰富员工业余生活,企业开展了形式多样的文艺活动,跳广场舞就是其中一项,经调查研究,其中750名员工积极参加活动(称为A类),另外250名员工不积极参加(称为B类),现用分层抽样方法(按A类,B类分二层)从全体员工中共抽查100名.
某企业有员工1000名,为了丰富员工业余生活,企业开展了形式多样的文艺活动,跳广场舞就是其中一项,经调查研究,其中750名员工积极参加活动(称为A类),另外250名员工不积极参加(称为B类),现用分层抽样方法(按A类,B类分二层)从全体员工中共抽查100名.| 满意度达标 | 满意度不达标 | 合 计 | |
| 积极参加活动 | 60 | ||
| 不积极参加活动 | 10 | ||
| 合 计 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知三棱柱ABC-A′B′C′中,平面BCC′B′⊥底面ABC,BB′⊥AC,底面ABC是边长为2的等边三角形,AA′=3,E、F分别在棱AA′,CC′上,且AE=C′F=2.
已知三棱柱ABC-A′B′C′中,平面BCC′B′⊥底面ABC,BB′⊥AC,底面ABC是边长为2的等边三角形,AA′=3,E、F分别在棱AA′,CC′上,且AE=C′F=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
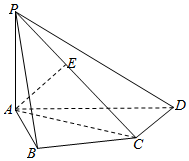 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com