
 已知三棱柱ABC-A′B′C′中,平面BCC′B′⊥底面ABC,BB′⊥AC,底面ABC是边长为2的等边三角形,AA′=3,E、F分别在棱AA′,CC′上,且AE=C′F=2.
已知三棱柱ABC-A′B′C′中,平面BCC′B′⊥底面ABC,BB′⊥AC,底面ABC是边长为2的等边三角形,AA′=3,E、F分别在棱AA′,CC′上,且AE=C′F=2.分析 (1)取BC中点O,先证AO⊥BC,再由面面垂直的性质定理证得AO⊥面BCC'B',再由线面垂直的判定定理即可得证;
(2)显然M不是A′,B′,棱A′B′上若存在一点M,使得C′M∥平面BEF,可通过线面平行的判断定理,即可证得;
(3)利用等体积转化,即可求棱锥A′-BEF的体积.
解答  (1)证明:取BC中点O,连接AO,因为三角形ABC是等边三角形,所以AO⊥BC,
(1)证明:取BC中点O,连接AO,因为三角形ABC是等边三角形,所以AO⊥BC,
又因为平面BCC′B′⊥底面ABC,AO?平面ABC,平面BCC′B′∩平面ABC=BC,
所以AO⊥平面BCC′B′,
又BB′?平面BCC′B,所以AO⊥BB′.
又BB′⊥AC,AO∩AC=A,AO?平面ABC,AC?平面ABC.
所以BB′⊥底面ABC.…(4分)
(2)解:显然M不是A′,B′,棱A′B′上若存在一点M,使得C′M∥平面BEF,
过M作MN∥AA′交BE于N,连接FN,MC′,所以MN∥CF,即C′M和FN共面,
所以C′M∥FN,
所以四边形C′MNF为平行四边形,所以MN=2,
所以MN是梯形A′B′BE的中位线,M为A′B′的中点.即$\frac{{{A^/}M}}{{M{B^/}}}=1$…(8分)
(3)解:${V_{{A^/}-BEF}}={V_{B-{A^/}EF}}=\frac{1}{3}×(\frac{1}{2}×1×2)×\sqrt{3}=\frac{{\sqrt{3}}}{3}$…(12分)
点评 本题考查线面平行和垂直的判定和性质,面面垂直的性质定理,以及三棱锥体积的计算,考查逻辑推理能力,属于中档题.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
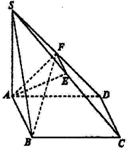 如图,四边形ABCD为矩形,SA⊥平面ABCD,E、F分别是SC、SD的中点,$SA=AD=2,AB=\sqrt{6}$,
如图,四边形ABCD为矩形,SA⊥平面ABCD,E、F分别是SC、SD的中点,$SA=AD=2,AB=\sqrt{6}$,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
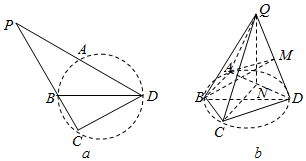 如图(a)已知线段BD=4,A,C关于BD对称,以BD为直径作圆,经过A,C两点,BA=2,延长DA,CB交于点P,将△PAB沿AB折起,使点P至点Q位置,得到图(b)所示空间图形,其中Q在平面ABCD内的射影恰为线段AD中点N,QD中点为M.
如图(a)已知线段BD=4,A,C关于BD对称,以BD为直径作圆,经过A,C两点,BA=2,延长DA,CB交于点P,将△PAB沿AB折起,使点P至点Q位置,得到图(b)所示空间图形,其中Q在平面ABCD内的射影恰为线段AD中点N,QD中点为M.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | m | 4 | 4.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com