
分析 (1)利用正弦定理和余弦定理化角为边,整理后可得a2+b2=c2.即△ABC是直角三角形;
(2)由(1)知,△ABC是以C为直角的直角三角形,且c=1,A=75°,可得C=15°,把边AC、BC分别用sin15°和cos15°表示,代入面积公式,再由二倍角正弦得答案.
解答 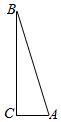 解:(1)由sinA+sinB=sinC(cosA+cosB),
解:(1)由sinA+sinB=sinC(cosA+cosB),
得a+b=c($\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}+\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$)=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2b}+\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2a}$,
即2a2b+2ab2=ab2+ac2-a3+a2b+bc2-b3,
∴a2b+ab2=ac2-a3+bc2-b3
∴b(a2+b2-c2)+a(a2+b2-c2)=0,
即(a+b)(a2+b2-c2)=0.
∵a+b≠0,
∴a2+b2-c2=0,即a2+b2=c2.
∴△ABC是直角三角形;
(2)由(1)知,△ABC是以C为直角的直角三角形,且c=1,A=75°,
∴B=15°,
则AC=sin15°,BC=cos15°,
∴${S}_{△ABC}=\frac{1}{2}AC•BC=\frac{1}{2}sin15°cos15°$=$\frac{1}{4}sin30°=\frac{1}{4}×\frac{1}{2}=\frac{1}{8}$.
点评 本题考查解三角形,考查了正弦定理和余弦定理的应用,考查了二倍角的正弦,是中档题.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:选择题
| A. | 8π | B. | $\frac{32}{3}$π | C. | $\frac{16}{3}$π | D. | 12π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若f(a)≤|b|,则a≤b | B. | 若f(a)≤2b,则a≤b | C. | 若f(a)≥|b|,则a≥b | D. | 若f(a)≥2b,则a≥b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某企业有员工1000名,为了丰富员工业余生活,企业开展了形式多样的文艺活动,跳广场舞就是其中一项,经调查研究,其中750名员工积极参加活动(称为A类),另外250名员工不积极参加(称为B类),现用分层抽样方法(按A类,B类分二层)从全体员工中共抽查100名.
某企业有员工1000名,为了丰富员工业余生活,企业开展了形式多样的文艺活动,跳广场舞就是其中一项,经调查研究,其中750名员工积极参加活动(称为A类),另外250名员工不积极参加(称为B类),现用分层抽样方法(按A类,B类分二层)从全体员工中共抽查100名.| 满意度达标 | 满意度不达标 | 合 计 | |
| 积极参加活动 | 60 | ||
| 不积极参加活动 | 10 | ||
| 合 计 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
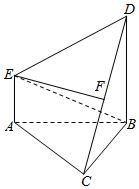 如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,CD与平面ABDE所成角的正弦值为$\frac{{\sqrt{6}}}{4}$.
如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,CD与平面ABDE所成角的正弦值为$\frac{{\sqrt{6}}}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com