
分析 (1)通过an+Sn=1与an-1+Sn-1=1(n≥2)作差,进而整理可知数列{an}是首项、公比均为$\frac{1}{2}$的等比数列,计算即得结论;
(2)通过${b_1}{c_1}+{b_2}{c_2}+…+{b_n}{c_n}=(2n-1){2^{n+1}}+2$与b1c1+b2c2+…+bn-1cn-1=(2n-3)2n+2作差,利用an=$\frac{1}{{2}^{n}}$可知bn=2n+1;
(3)通过(1)可知${d_n}=\frac{1}{a_n}-1$=2n-1,进而裂项、放缩可知$\frac{{d}_{n}}{{d}_{n+1}}$≥$\frac{1}{2}$-$\frac{1}{3}$×$\frac{1}{{2}^{n}}$,然后相加、化简即得结论.
解答 (1)解:∵an+Sn=1,
∴an-1+Sn-1=1(n≥2),
两式相减得:an=$\frac{1}{2}$an-1(n≥2),
又∵a1+S1=1,即a1=$\frac{1}{2}$,
∴数列{an}是首项、公比均为$\frac{1}{2}$的等比数列,
∴其通项公式an=$\frac{1}{{2}^{n}}$;
(2)解:∵${b_1}{c_1}+{b_2}{c_2}+…+{b_n}{c_n}=(2n-1){2^{n+1}}+2$,
∴b1c1+b2c2+…+bn-1cn-1=(2n-3)2n+2,
两式相减得:bncn=(2n+1)2n,
由(1)可知${c_n}=\frac{1}{a_n}$=2n,故bn=2n+1(n≥2),
又∵b1c1=6,即b1=3满足上式,
∴bn=2n+1;
(3)证明:由(1)可知${d_n}=\frac{1}{a_n}-1$=2n-1,
∵$\frac{{d}_{n}}{{d}_{n+1}}$=$\frac{{2}^{n}-1}{{2}^{n+1}-1}$=$\frac{1}{2}$-$\frac{1}{2({2}^{n+1}-1)}$=$\frac{1}{2}$-$\frac{1}{3×{2}^{n}+{2}^{n}-2}$≥$\frac{1}{2}$-$\frac{1}{3}$×$\frac{1}{{2}^{n}}$,
∴$\frac{{d}_{1}}{{d}_{2}}$+$\frac{{d}_{2}}{{d}_{3}}$+…+$\frac{{d}_{n}}{{d}_{n+1}}$≥n×$\frac{1}{2}$-$\frac{1}{3}$×($\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$)=$\frac{n}{2}$-$\frac{1}{3}$(1-$\frac{1}{{2}^{n}}$)>$\frac{n}{2}$-$\frac{1}{3}$,
即$\frac{d_1}{d_2}+\frac{d_2}{d_3}+…+\frac{d_n}{{{d_{n+1}}}}>\frac{n}{2}-\frac{1}{3}$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
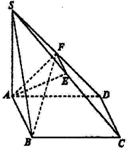 如图,四边形ABCD为矩形,SA⊥平面ABCD,E、F分别是SC、SD的中点,$SA=AD=2,AB=\sqrt{6}$,
如图,四边形ABCD为矩形,SA⊥平面ABCD,E、F分别是SC、SD的中点,$SA=AD=2,AB=\sqrt{6}$,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
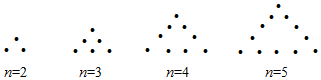
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | m | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:(单位:万元)
为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:(单位:万元)| 收入x | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
| 支出y | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
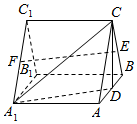 如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等,D,E,F分别为棱AB,BC,A1C1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等,D,E,F分别为棱AB,BC,A1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,-$\frac{1}{2}$] | B. | [-1,0] | C. | [0,1] | D. | [1,$\frac{3}{2}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com