
 为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:(单位:万元)
为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:(单位:万元)| 收入x | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
| 支出y | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
分析 (1)分别以x,y为横纵坐标描点;
(2)计算样本中心,代入回归方程求出$\stackrel{∧}{a}$,得出回归方程;
(3)把x=15代入回归方程计算$\stackrel{∧}{y}$.
解答 解:(1)作出散点图如图所示:
(2)$\overline x=\frac{8.2+8.6+10.0+11.3+11.9}{5}=10$,
$\overline{y}=\frac{6.2+7.5+8.0+8.5+9.8}{5}$=8.
∴$\stackrel{∧}{a}$=8-0.76×10=0.4.
所以回归直线方程为$\stackrel{∧}{y}$=0.76x+0.4.
(3)当x=15时,$\stackrel{∧}{y}$=0.76×15+0.4=11.8万元.
答:可预测该社区一户年收入为15万元家庭年支出为11.8万元.
点评 本题考查了线性回归方程的求解及数值预测,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
 如图所示,在△ABC中,D为边AC的中点,BC=3BE,其中AE与BD交于O点,延长CO交边AB于F点,则$\frac{FO}{OC}$=$\frac{1}{3}$.
如图所示,在△ABC中,D为边AC的中点,BC=3BE,其中AE与BD交于O点,延长CO交边AB于F点,则$\frac{FO}{OC}$=$\frac{1}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,长方体ABCD-A1B1C1D1中,AB=AD=1.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 128块 | B. | 126块 | C. | 64块 | D. | 62块 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2)(3) | B. | (1)(4)(5) | C. | (1)(2)(3) | D. | (2)(3)(4)(5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
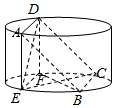 如图所示,圆柱的高为2,底面半径为$\sqrt{7}$,AE,DF是圆柱的两条母线,过AD做圆柱的截面交下底面于BC,四边形ABCD是正方形.
如图所示,圆柱的高为2,底面半径为$\sqrt{7}$,AE,DF是圆柱的两条母线,过AD做圆柱的截面交下底面于BC,四边形ABCD是正方形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com