
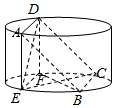
 如图所示,圆柱的高为2,底面半径为$\sqrt{7}$,AE,DF是圆柱的两条母线,过AD做圆柱的截面交下底面于BC,四边形ABCD是正方形.
如图所示,圆柱的高为2,底面半径为$\sqrt{7}$,AE,DF是圆柱的两条母线,过AD做圆柱的截面交下底面于BC,四边形ABCD是正方形.分析 (I)由圆柱母线垂直底面得AE⊥BC,又BC⊥AB,得出BC⊥平面ABE,于是BC⊥BE;
(II)过E作EO⊥AB,则可证EO⊥平面ABCD,设正方形边长为x,求出BE,在Rt△BCE中利用勾股定理列方程解出x,代入棱锥的体积公式计算.
解答  证明:(I)∵AE是圆柱的母线,
证明:(I)∵AE是圆柱的母线,
∴AE⊥底面BCFE,∵BC?平面BCFE,
∴AE⊥BC,
∵四边形ABCD是正方形,
∴BC⊥AB,
又AB?平面ABE,AE?平面ABE,AB∩AE=A,
∴BC⊥平面ABE,∵BE?平面ABE,
∴BC⊥BE.
(II)过E作EO⊥AB于O,
由(I)知BC⊥平面ABE,∵EO?平面ABE,
∴BC⊥EO,又AB?平面ABCD,BC?平面ABCD,AB∩BC=B,
∴EO⊥平面ABCD.
设正方形ABCD的边长为x,则AB=BC=x,
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=$\sqrt{{x}^{2}-4}$,
∵BC⊥BE,∴EC为圆柱底面直径,即EC=2$\sqrt{7}$.
∵BE2+BC2=EC2,即x2-4+x2=28,解得x=4,
∴BE=2$\sqrt{3}$,EO=$\frac{AE•BE}{AB}=\sqrt{3}$,S正方形ABCD=16,
∴VE-ABCD=$\frac{1}{3}{S}_{正方形ABCD}•EO$=$\frac{1}{3}×16×\sqrt{3}$=$\frac{16\sqrt{3}}{3}$.
点评 本题考查了线面垂直的判定与性质,棱锥的体积计算,属于中档题.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:解答题
 为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:(单位:万元)
为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:(单位:万元)| 收入x | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
| 支出y | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16($π-\sqrt{3}$) | B. | 16($π-\sqrt{2}$) | C. | 8(2$π-3\sqrt{2}$) | D. | 8(2$π-\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,-$\frac{1}{2}$] | B. | [-1,0] | C. | [0,1] | D. | [1,$\frac{3}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知正棱锥P-ABCD中,PA⊥平面ABCD,△PAC为等腰直角三角形,PA=6,底面ABCD为平行四边形,且∠ABC+∠ADC=90°,E为线段AD的中点,F在线段PD上运动,记$\frac{PF}{PD}$=λ.
已知正棱锥P-ABCD中,PA⊥平面ABCD,△PAC为等腰直角三角形,PA=6,底面ABCD为平行四边形,且∠ABC+∠ADC=90°,E为线段AD的中点,F在线段PD上运动,记$\frac{PF}{PD}$=λ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com