
分析 求得f(x)的导数,由f′(1)=3,可得a=0,求出f(x)的解析式和导数,可得所求切线的斜率和切点,运用点斜式方程,可得所求切线的方程.
解答 解:函数f(x)=x2(x-a)的导数为
f′(x)=2x(x-a)+x2=3x2-2ax,
f′(1)=3,即为3-2a=3,
解得a=0,即f(x)=x3,f′(x)=3x2,
可得曲线y=f(x)在点(1,f(1))处的切线斜率为3,
切点为(1,1),
即有切线的方程为y-1=3(x-1),
即为3x-y-2=0.
故答案为:3x-y-2=0.
点评 本题考查导数的运用:求切线的方程,考查导数的几何意义:函数在某点处的导数即为曲线在该点处的切线的斜率,正确求导和运用点斜式方程是解题的关键,属于基础题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
| X1 | 6 | 7 | 8 | 9 | 10 |
| P | 0.16 | 0.14 | 0.42 | 0.1 | 0.18 |
| X2 | 6 | 7 | 8 | 9 | 10 |
| P | 0.19 | 0.24 | 0.12 | 0.28 | 0.17 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
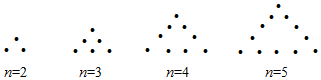
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
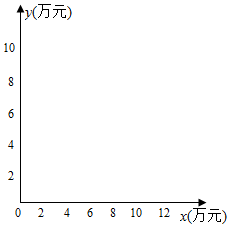 为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:(单位:万元)
为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:(单位:万元)| 收入x | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
| 支出y | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
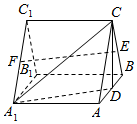 如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等,D,E,F分别为棱AB,BC,A1C1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等,D,E,F分别为棱AB,BC,A1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | 2π | C. | 3π | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知正棱锥P-ABCD中,PA⊥平面ABCD,△PAC为等腰直角三角形,PA=6,底面ABCD为平行四边形,且∠ABC+∠ADC=90°,E为线段AD的中点,F在线段PD上运动,记$\frac{PF}{PD}$=λ.
已知正棱锥P-ABCD中,PA⊥平面ABCD,△PAC为等腰直角三角形,PA=6,底面ABCD为平行四边形,且∠ABC+∠ADC=90°,E为线段AD的中点,F在线段PD上运动,记$\frac{PF}{PD}$=λ.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com