
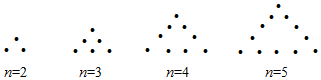
分析 根据题意,可得a2=3=3×(2-1),a3=6=3×(3-1),a4=9=3×(4-1),a5=12=3×(5-1)…an=3(n-1),数列{an}是首项为3,公差为3的等差数列,通项为an=3(n-1)(n≥2),所以$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{3(n-1)•3n}$=$\frac{1}{9}$($\frac{1}{n-1}$-$\frac{1}{n}$),据此解答即可.
解答 解:根据分析,可得
a2=3=3×(2-1),a3=6=3×(3-1),a4=9=3×(4-1),a5=12=3×(5-1)…an=3(n-1),
数列{an}是首项为3,公差为3的等差数列,通项为an=3(n-1)(n≥2);
所以$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{3(n-1)•3n}$=$\frac{1}{9}$($\frac{1}{n-1}$-$\frac{1}{n}$),
则$\frac{9}{{a}_{2}{a}_{3}}$+$\frac{9}{{a}_{3}{a}_{4}}$+$\frac{9}{{a}_{4}{a}_{5}}$+…+$\frac{9}{{a}_{2015}{a}_{2016}}$=1-$\frac{1}{2}$+$\frac{1}{2}-\frac{1}{3}$+…+$\frac{1}{2014}$-$\frac{1}{2015}$=$\frac{2014}{2015}$.
故答案为:$\frac{2014}{2015}$.
点评 本题主要考查了图形的变化类,解答此题的关键是根据已知的图形中点数的变化推得an=3(n-1)(n≥2).


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 若f(a)≤|b|,则a≤b | B. | 若f(a)≤2b,则a≤b | C. | 若f(a)≥|b|,则a≥b | D. | 若f(a)≥2b,则a≥b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
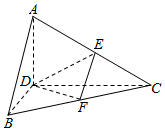 正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,长方体ABCD-A1B1C1D1中,AB=AD=1.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
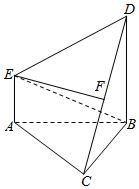 如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,CD与平面ABDE所成角的正弦值为$\frac{{\sqrt{6}}}{4}$.
如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,CD与平面ABDE所成角的正弦值为$\frac{{\sqrt{6}}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 128块 | B. | 126块 | C. | 64块 | D. | 62块 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com