练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．某地政府决定用同规格大理石建一堵七层的护墙，各层用该种大理石块数是：第一层用全部大理石的一半多一块，第二层用剩下的一半多一块，第三层…以此类推，到第七层恰好将大理石用完，则共需该种大理石（　　）
    A．128块B．126块C．64块D．62块

    分析 每一层都用去了上次剩下砖块的一半多一块，由题设知到第7层恰好砖用光，且每一层都用去了前一层剩下的一半多一块，从而得出第7层用了2块，第6层用4块，第5层用了8块，…，以此类推，能求出此次砌墙一共用了多少块砖．

    解答 解：由已知中每一层都用去了上次剩下砖块的一半多一块，
    且第7层恰好砖用光，
    故第7层用了2块，
    第6层用4块，
    第5层用了8块，
    …，
    第1层用了26块，
    故共需该种大理石2+4+8+…+26=27-2=126块，
    故选：B

    点评 本题考查等差数列的通项公式，考查了等差数列的前n项和，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    2．函数f（x）=2x+x3-2在区间（0，1）内的零点个数是（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

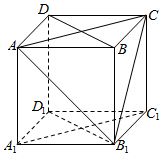    7．如图，在棱长为1的正方体ABCD-A1B1C1D1中．
    （1）求异面直线BC1与AA1所成的角的大小；
    （2）求三棱锥B1-A1C1B的体积；
    （3）求证：BD1⊥面AB1C．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

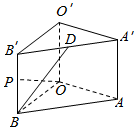    4．如图所示，在直三棱柱ABO-A′B′O′中，OO′=4，OA=4，OB=3，∠AOB=90°，D是线段A′B′的中点，P是侧棱BB′上的一点，若OP⊥BD，求OP与底面AOB所成角的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．若图所示，将若干个点摆成三角形图案，每条边（包括两个端点）n（n＞1，n∈N*）个点，相应的图案中总的点数记为an，则$\frac{9}{{a}_{2}{a}_{3}}$+$\frac{9}{{a}_{3}{a}_{4}}$+$\frac{9}{{a}_{4}{a}_{5}}$+…+$\frac{9}{{a}_{2015}{a}_{2016}}$=$\frac{2014}{2015}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知正三棱柱ABC-A1B1C1的体积为$\frac{{9\sqrt{3}}}{4}$，底面边长为3，若O为底面A1B1C1的中心，则OA与平面ABC所成角的大小为$\frac{π}{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

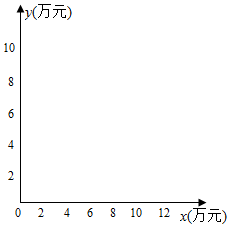    8．为了解某社区居民的家庭年收入与年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：（单位：万元）
    收入x8.28.610.011.311.9
    支出y6.27.58.08.59.8
    （1）请画出上表数据的散点图；（3）试根据（2）求出的线性回归方程，预测该社区一户收入为15万元家庭年支出为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．在平行四边形ABCD中，AB⊥BD，AB=1，BD=$\sqrt{2}$，若将其沿BD折成直二面角A-BD-C，则三棱锥A-BDC的外接球的表面积为（　　）
    A．πB．2πC．3πD．4π

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．半径为2的球O中有一内接正四棱柱（底面是正方形，侧棱垂直底面），当该正四棱柱的侧面积最大时，球的表面积与该正四棱柱的侧面积之差是（　　）
    A．16（$π-\sqrt{3}$）B．16（$π-\sqrt{2}$）C．8（2$π-3\sqrt{2}$）D．8（2$π-\sqrt{3}$）

    查看答案和解析>>

    同步练习册答案