
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 设B的坐标,求出A,B的中点坐标C,利用C在g(x)上,建立方程关系,转化为两个函数的交点个数问题 进行求解即可.
解答 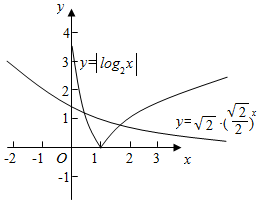 解:令点B(x,|log2x|),x>0,
解:令点B(x,|log2x|),x>0,
A,B的中点C($\frac{1+x}{2}$,$\frac{1}{2}$|log2x|).
由于点C在函数g(x)=($\frac{1}{2}$)x的图象上,
故有$\frac{1}{2}$|log2x|=($\frac{1}{2}$)${\;}^{\frac{1+x}{2}}$=$\frac{\sqrt{2}}{2}$•($\frac{\sqrt{2}}{2}$)x,
即|log2x|=$\sqrt{2}$•($\frac{\sqrt{2}}{2}$)x,
故函数f(x)关于函数g(x)的“关联点”的个数是,
即为函数y=|log2x|和曲线y=$\sqrt{2}$•($\frac{\sqrt{2}}{2}$)x的交点的个数.
在同一个坐标系中,画出函数y=|log2x|和y=$\sqrt{2}$•($\frac{\sqrt{2}}{2}$)x的$\frac{4}{1+x}$的图象,
由图象知两个函数的交点个数为2个,
则函数f(x)关于函数g(x)的“关联点”的个数是2,
故故选:B.
点评 本题主要考查新定义,关联点的个数的求法,方程根的存在性以及个数判断,体现了转化、数形结合的数学思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 144 | B. | 288 | C. | 480 | D. | 720 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某商店有标号为0到9的10个气球
某商店有标号为0到9的10个气球查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (1,4) | C. | (2,4) | D. | (4,8) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com