
分析 (1)根据平面向量的坐标运算以及单位向量的概念,求出答案即可;
(2)设出点D的坐标,利用向量共线与模长公式,列出方程组求出点D的坐标;
(3)设处点D的坐标,利用平行四边形表示的向量相等,列出方程组求出点D的坐标.
解答 解:(1)∵点A(4,-2),B(-4,4),C(1,1),
∴$\overrightarrow{AB}$=(-8,6),|$\overrightarrow{AB}$|=$\sqrt{{(-8)}^{2}{+6}^{2}}$=10,
∴方向与$\overrightarrow{AB}$一致的单位向量是$\overrightarrow{i}$=$\frac{\overrightarrow{AB}}{|AB|}$=(-$\frac{4}{5}$,$\frac{3}{5}$);
(2)设点D(x,y),则$\overrightarrow{CD}$=(x-1,y-1),
又$\overrightarrow{CD}$与$\overrightarrow{AB}$共线,且|$\overrightarrow{CD}$|=4,
则$\left\{\begin{array}{l}{6(x-1)+8(y-1)=0}\\{\sqrt{{(x-1)}^{2}{+(y-1)}^{2}}=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{21}{5}}\\{y=-\frac{7}{5}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{11}{5}}\\{y=\frac{17}{5}}\end{array}\right.$,
∴点D的坐标为($\frac{21}{5}$,-$\frac{7}{5}$)或(-$\frac{11}{5}$,$\frac{17}{5}$);
(3)设点D(x,y),∵A,B,C都是某个平行四边形的顶点,
当$\overrightarrow{AB}$=$\overrightarrow{DC}$时,(1-x,1-y)=(-8,6),
即$\left\{\begin{array}{l}{1-x=-8}\\{1-y=6}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=9}\\{y=-5}\end{array}\right.$,
∴顶点D的坐标为(9,-5);
当$\overrightarrow{AC}$=$\overrightarrow{DB}$时,(-4-x,4-y)=(-3,3),
即$\left\{\begin{array}{l}{-4-x=-3}\\{4-y=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$,
∴顶点D的坐标为(-1,1);
综上顶点D的坐标为(9,-5)或(-1,1).
点评 本题考查了平面向量的坐标运算与应用问题,也考查了方程思想的应用问题,是综合性题目.


科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{2}$个单位长度 | B. | 向右平移$\frac{π}{4}$个单位长度 | ||
| C. | 向左平移$\frac{π}{4}$个单位长度 | D. | 向右平移$\frac{π}{2}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>1 | B. | a≤1 | C. | a≤-$\frac{\sqrt{2}}{2}$ | D. | a$≤\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值3+4$\sqrt{3}$ | B. | 最小值3+4$\sqrt{3}$ | C. | 最大值3+2$\sqrt{3}$ | D. | 最小值3+2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
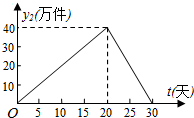 我市某外资企业生产的一批产品上市后30天内全部售完,该企业对这批产品上市后每天的销售情况进行了跟踪调查.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如下表所示.而国外市场的日销售量y2(万件)与时间t(t为整数,单位:天)的关系如图所示.
我市某外资企业生产的一批产品上市后30天内全部售完,该企业对这批产品上市后每天的销售情况进行了跟踪调查.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如下表所示.而国外市场的日销售量y2(万件)与时间t(t为整数,单位:天)的关系如图所示.| 时间t(天) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| 日销售量y1(万件) | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 二次函数y=ax2+bx+c的图象如图所示,下列结论:a+b+c>0;②a-b+c>0;③abc<0;④2a-b=0,其中正确的个数是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论:a+b+c>0;②a-b+c>0;③abc<0;④2a-b=0,其中正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com